题目内容
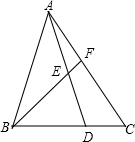 如图,△ABC的面积为60,点D在BC上,BD=2CD,连接AD,点E为AD中点,连接BE并延长交AC于点F,则△AEF的面积为
如图,△ABC的面积为60,点D在BC上,BD=2CD,连接AD,点E为AD中点,连接BE并延长交AC于点F,则△AEF的面积为
- A.2
- B.4
- C.5
- D.8
B
分析:先过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,由于△ABC的面积为60,BD=2CD,可求S△ABD,S△ACD,又E是AD中点,可求S△ABE.在△ADG中,DG∥BF,E是AD中点,利用平行线分线段成比例定理的推论,可知AF=FG,从而可知△AEF∽△ADG,再利用相似三角形的面积比等于相似比的平方,可得∴S△ADG=4x,同理可求S△BCF=9y,再利用三角形面积之间的加减关系可得关于x、y的二元一次方程,解即可.
解答:过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,
∵△ABC的面积为60,BD=2CD,
∴S△ABD= ×S△ABC=40,
×S△ABC=40,
S△ACD= ×S△ACD=20,
×S△ACD=20,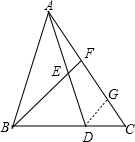
又∵E是AD中点,
∴S△ABE=S△BDE= ×S△ABD=20,
×S△ABD=20,
在△ADG中,∵DG∥BF,E是AD中点,
∴S△AEF:S△ADG=1:4,
∴S△ADG=4x,
同理在△BCF中,∵DG∥BF,BD=2CD,
∴S△BCF=9y,
那么有
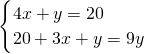 ,
,
解得
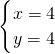 ,
,
故选B.
点评:本题考查了三角形的面积计算、平行线分线段成比例的推论、相似三角形的判定、相似三角形的面积比等于相似比的平方.关键是作辅助线,所作的平行线能用到两个三角形中.
分析:先过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,由于△ABC的面积为60,BD=2CD,可求S△ABD,S△ACD,又E是AD中点,可求S△ABE.在△ADG中,DG∥BF,E是AD中点,利用平行线分线段成比例定理的推论,可知AF=FG,从而可知△AEF∽△ADG,再利用相似三角形的面积比等于相似比的平方,可得∴S△ADG=4x,同理可求S△BCF=9y,再利用三角形面积之间的加减关系可得关于x、y的二元一次方程,解即可.
解答:过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,
∵△ABC的面积为60,BD=2CD,
∴S△ABD=
 ×S△ABC=40,
×S△ABC=40,S△ACD=
 ×S△ACD=20,
×S△ACD=20,
又∵E是AD中点,
∴S△ABE=S△BDE=
 ×S△ABD=20,
×S△ABD=20,在△ADG中,∵DG∥BF,E是AD中点,
∴S△AEF:S△ADG=1:4,
∴S△ADG=4x,
同理在△BCF中,∵DG∥BF,BD=2CD,
∴S△BCF=9y,
那么有
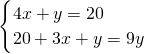 ,
,解得
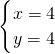 ,
,故选B.
点评:本题考查了三角形的面积计算、平行线分线段成比例的推论、相似三角形的判定、相似三角形的面积比等于相似比的平方.关键是作辅助线,所作的平行线能用到两个三角形中.

练习册系列答案
相关题目
 如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是
如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为 如图,△ABC的面积为
如图,△ABC的面积为 3、如图,△ABC的面积为1,若把△ABC的各边分别延长一倍,得到一个新的△DEF,则S△DEF=
3、如图,△ABC的面积为1,若把△ABC的各边分别延长一倍,得到一个新的△DEF,则S△DEF= 如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连结A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连结A2,B2,C2,得到△A2B2C2.…按此规律,要使得到的三角形的面积超过2013,最少经过
如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连结A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连结A2,B2,C2,得到△A2B2C2.…按此规律,要使得到的三角形的面积超过2013,最少经过