题目内容
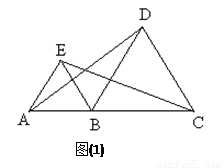
如图(1),点A、B、C在同一直线上,且△ABE, △BCD都是等边三角形,连结AD,CE.
(1)△BEC可由△ABD顺时针旋转得到吗?若是,请描述这一旋转变换过程;若不是,请说明理由;
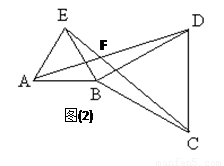
(2)若△BCD绕点B顺时针旋转,使点A,B,C不在同一直线上(如图(2)),则在旋转过程中:
①线段AD与EC的长度相等吗?请说明理由.
②锐角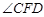 的度数是否改变?若不变,请求出
的度数是否改变?若不变,请求出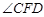 的度数;若改变,请说明理由.
的度数;若改变,请说明理由.
(注:等边三角形的三条边都相等,三个角都是60°)
【答案】
(1)△BEC可以由△ABD绕点B顺时针旋转60°得到.
(2) 说明△ABD≌△EBC (SAS)得AD=EC
②锐角 的度数不改变。
的度数不改变。
∵△ABD≌△EBC
∴∠BCE=∠BDA
∴∠FCD + ∠FDC =∠FCD + ∠BDC +∠ADB=∠BCE + ∠FCD + ∠BDC=∠BCD + ∠BDC=60°+ 60°=120°
∴∠CFD=180°-(∠FCD + ∠FDC) = 180°-120°= 60°
【解析】(1)根据等边三角形的性质得到BA=BE,BD=BC,∠ABE=∠CBD=60°,则∠ABD=∠EBC,根据旋转的定义得到△ABD绕点B顺时针旋转60°可得到△BEC;
(2)根据等边三角形的性质得到BA=BE,BD=BC,∠ABE=∠CBD=60°,则∠ABD=∠EBC,易证得△ABD≌△EBC,根据全等的旋转即可得到AD=EC;
(3)由△ABD≌△EBC得到∠BCE=∠BDA,则有∠FCD+∠FDC=∠FCD+∠BDC+∠ADB=∠BCE+∠FCD+∠BDC=∠BCD+∠BDC=60°+60°=120°,根据三角形内角和定理即可得到∠CFD的度数.

练习册系列答案
相关题目
 两个反比例函数y=
两个反比例函数y=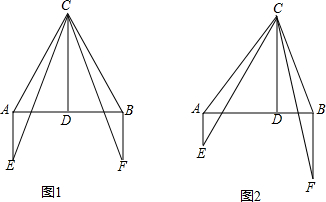
 如图,已知点C在线段AB上,以AC和CB为边,在AB的同侧分别作正三角形△AMC和△CNB,连接AN和BM分别交MC、NC于P、G.
如图,已知点C在线段AB上,以AC和CB为边,在AB的同侧分别作正三角形△AMC和△CNB,连接AN和BM分别交MC、NC于P、G. 作图题:如图,已知点C是∠AOB的边OB上的一点.求作⊙P,使它与OA、OB相切,且圆心P到点O、C的距离相等(保留作图痕迹,不写作法).
作图题:如图,已知点C是∠AOB的边OB上的一点.求作⊙P,使它与OA、OB相切,且圆心P到点O、C的距离相等(保留作图痕迹,不写作法).