题目内容
【题目】如图，抛物线 
与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，连接BC．
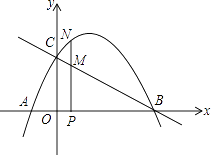
（1）求点A、B、C的坐标．
（2）点P为AB上的动点（点A、O、B除外），过点P作直线PN⊥x轴，交抛物线于点N，交直线BC于点M．设点P到原点的值为t，MN的长度为s，求s与t的函数关系式．
（3）在（2）的条件下，试求出在点P运动的过程中，由点O、P、N围成的三角形与Rt△COB相似时点P的坐标．
【答案】
（1）
解：∵点A、B、C在二次函数图象上
∴把x=0代入 
，得y=2
把y=0代入 ，得x1=﹣1，x2=4，
∴A（﹣1，0），B（4，0），C（0，2）；
（2）
解：设直线BC的解析式为y=kx+b（k≠0），
把B（4，0），C（0，2）代入，得 
， 
∴直线BC的解析式为 
∵OP=t
∴P（t，0），M（t，﹣ 
t+2），N（t，﹣ t2+ 
t+2），
如图，
∴S1=N1P1﹣M1P1=﹣ t2+ t+2﹣（﹣ t+2）=﹣ t2+2t（0＜t＜4），
S2=M2P2﹣N2P2=﹣ t+2﹣（﹣ t2+ t+2）= t2﹣2t（﹣1＜t＜0），
（3）
解：如图，
①若△OPN∽△OCB，当OP与OC是对应边时，则 
，即 
化简得：t2+t﹣4=0，
解得： 
， 
（不合题意，舍去）
②若△OPN∽△OBC，当OP与OB是对应边时，则 
，即 
化简得：t2﹣2t﹣4=0
解得：t3=1+ 
，t4=1﹣ （不合题意，舍去）
∴符合题意的点P的坐标为（ 
，0）和（1+ ，0）．
【解析】（1）分别令y=0、x=0即可以求出A、B、C的坐标，（2）应分为点P在y轴的左侧和点P在y轴的右侧两种情况，分别求s与t的函数关系式，MN的长就是M、N两点纵坐标的差，（3）在没有确定对应关系的情况下，两三角形相似应分两种情况讨论解决．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
