题目内容
【题目】在正方形ABCD中，AB=8，点P在边CD上，tan∠PBC=
，点Q是在射线BP上的一个动点，过点Q作AB的平行线交射线AD于点M，点R在射线AD上，使RQ始终与直线BP垂直．
（1）如图1，当点R与点D重合时，求PQ的长；
（2）如图2，试探索： 
的比值是否随点Q的运动而发生变化？若有变化，请说明你的理由；若没有变化，请求出它的比值；
（3）如图3，若点Q在线段BP上，设PQ=x，RM=y，求y关于x的函数关系式，并写出它的定义域．
【答案】（1）
；（2）
；（3）
；0≤x≤
.
【解析】试题分析：（1）由正方形的性质及
可求出BC=8，PC=6，由勾股定理可求出BP=10，再由△
∽△
即可求出结论；
（2）由正方形的性质得∠A=∠ABC=∠C=90°，由MQ∥AB得∠QMR=∠A，故∠QMR=∠C；由MQ∥AB得
，而∠1+∠RQM=90°,∠ABP+∠PBC=90°，故
，从而△
∽△
.故可得出结论；
（3）延长
交
的延长线于点
，通过证明
，分别计算
及
, 
，从而可得出结论.
试题解析：（1）由题意，得
,
在Rt△
中， 
∴
∵
∴
∴
∴
∵
∴
∴
∵
∴△
∽△
∴
∴
∴
（2）答： 
的比值随点
的运动没有变化
理由：如图，
∵
∥
∴
, 
∵
∴
∵
∴
∴
∴△
∽△
∴
∵
， 
∴
∴
的比值随点
的运动没有变化,比值为
（3）延长
交
的延长线于点
∵
∥
∴
∵
∴
∴
∴
∵
∥
, 
∥
∴
∥
∴
∵
, 
∴
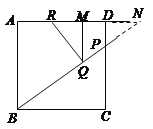
又
, 
∴
∴
它的定义域是
【题目】某快车的计费规则如表1，小明几次乘坐快车的情况如表2，请仔细观察分析表格解答以下问题：
（1）填空：a＝ ，b＝ ；
（2）列方程求解表1中的x；
（3）小明的爸爸23：10打快车从机场回家，快车行驶的平均速度是100公里/小时，到家后小明爸爸支付车费603元，请问机场到小明家的路程是多少公里？（用方程解决此问题）
表1：某快车的计费规则
里程费（元/公里） | 时长费（元/分钟） | 远途费（元/公里） | |||
5：00﹣23：00 | a | 9：00﹣18：00 | x | 12公里及以下 | 0 |
23：00﹣次日5：00 | 3.2 | 18：00﹣次日9：00 | 0.5 | 超出12公里的部分 | 1.6 |
（说明：总费用＝里程费+时长费+远途费）
表2：小明几次乘坐快车信息
上车时间 | 里程（公里） | 时长（分钟） | 远途费（元） | 总费用（元） |
7：30 | 5 | 5 | 0 | 13.5 |
10：05 | 20 | 18 | 66.7 |
