题目内容
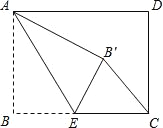
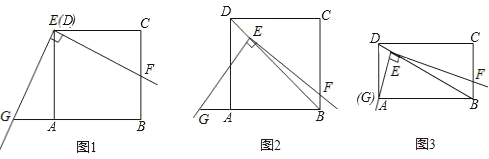
【题目】直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() 为⊙
为⊙![]() 的直径,动点
的直径,动点![]() 沿
沿![]() 方向从点
方向从点![]() 开始向点
开始向点![]() 以
以![]() 的速度运动,动点
的速度运动,动点![]() 沿
沿![]() 方向从点
方向从点![]() 开始向点
开始向点![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发,当其中一点停止时,另一点也随之停止运动.
两点同时出发,当其中一点停止时,另一点也随之停止运动.

(![]() )求⊙
)求⊙![]() 的直径.
的直径.
(![]() )当
)当![]() 为何值时,四边形
为何值时,四边形为等腰梯形?
(![]() )是否存在某一时刻
)是否存在某一时刻![]() ,使直线
,使直线![]() 与⊙
与⊙![]() 相切?若存在,求出
相切?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(![]() )⊙
)⊙![]() 直径为
直径为![]() ;(
;(![]() )
)![]() ;(
;(![]() )存在,
)存在,![]() 时,
时,![]() 与⊙
与⊙![]() 相切.
相切.
【解析】(![]() )⊙
)⊙![]() 直径为
直径为![]() .
.
(![]() )
)![]() .
.
(![]() )存在,
)存在,![]() 时,
时,![]() 与⊙
与⊙![]() 相切.
相切.
试题分析:(1)过点![]() 作
作![]() 于
于![]() ,在
,在![]() 中,利用勾股定理求DE.(2) 当四边形
中,利用勾股定理求DE.(2) 当四边形![]() 为等腰梯形时,
为等腰梯形时,![]() ,代入求值.(3) 存在,若
,代入求值.(3) 存在,若![]() 与⊙
与⊙![]() 相切,切点为
相切,切点为![]() ,作
,作![]() 于
于![]() ,
,![]() ,用t表示PQ,OH,勾股定理得
,用t表示PQ,OH,勾股定理得![]() ,
,
求t.
试题解析:

(![]() )过点
)过点![]() 作
作![]() 于
于![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() ,
,
在![]() 中.
中.
∵![]() ,
,
∴![]() .
.
∴⊙![]() 的直径为
的直径为![]() .
.
(![]() )由题意知
)由题意知
![]() ,
,![]() .
.
当四边形![]() 为等腰梯形时,
为等腰梯形时,
![]() .
.
∵![]()
解得![]() .
.
(![]() )存在,若
)存在,若![]() 与⊙
与⊙![]() 相切,切点为
相切,切点为![]() ,作
,作![]() 于
于![]() .
.
∴![]()
![]() .
.
又![]() ,
,
![]() ,
,
勾股定理得![]() ,
,
即![]() ,
,
解得![]() ,
,![]() .
.
又∵![]() ,
,![]() 都符合.
都符合.
综上所述,![]() 时,
时,![]() 与⊙
与⊙![]() 相切.
相切.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目