题目内容
如图，AB⊥BC，DE∥BC，若∠BED=120°，那么∠ABE=________．
30°
分析：由DE∥BC与∠BED=120°，根据两直线平行，同旁内角互补，即可求得∠EBC的度数，又由AB⊥BC，即可求得∠ABE的度数．
解答：∵DE∥BC，
∴∠BED+∠EBC=180°，
∵∠BED=120°，
∴∠EBC=60°，
∵AB⊥BC，
∴∠ABC=90°，
∴∠ABE=30°．
故答案为：30°．
点评：此题考查了平行线的性质与垂直的定义．解题的关键是掌握两直线平行，同旁内角互补定理的应用．
分析：由DE∥BC与∠BED=120°，根据两直线平行，同旁内角互补，即可求得∠EBC的度数，又由AB⊥BC，即可求得∠ABE的度数．
解答：∵DE∥BC，
∴∠BED+∠EBC=180°，
∵∠BED=120°，
∴∠EBC=60°，
∵AB⊥BC，
∴∠ABC=90°，
∴∠ABE=30°．
故答案为：30°．
点评：此题考查了平行线的性质与垂直的定义．解题的关键是掌握两直线平行，同旁内角互补定理的应用．
练习册系列答案
相关题目
已知：如图，AB=BC=CA=AD，AH⊥CD于H，CP⊥BC，CP交AH于P．求证：△ABC的面积S=
12、如图，AB=BC=CD，且∠A=15°，则∠ECD=（ ）
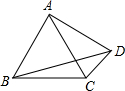如图，AB=BC=AC=AD，那么∠BDC等于（ ）
如图，AB=BC=CD=DE=1，且BC⊥AB，CD⊥AC，DE⊥AD，则线段AE的长为