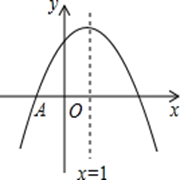题目内容
如图,已知二次函数 (m>0)的图象与x轴交于A、B两点.
(m>0)的图象与x轴交于A、B两点.

(1)写出A、B两点的坐标(坐标用m表示);
(2)若二次函数图象的顶点P在以AB为直径的圆上,求二次函数的解析式;
(3)设以AB为直径的⊙M与y轴交于C、D两点,求CD的长.
 (m>0)的图象与x轴交于A、B两点.
(m>0)的图象与x轴交于A、B两点.
(1)写出A、B两点的坐标(坐标用m表示);
(2)若二次函数图象的顶点P在以AB为直径的圆上,求二次函数的解析式;
(3)设以AB为直径的⊙M与y轴交于C、D两点,求CD的长.
解:(1)∵ ,∴当y=0时,
,∴当y=0时, 。
。
解得x1=﹣m,x2=3m。
∵m>0,∴A、B两点的坐标分别是(﹣m,0),(3m,0)。
(2)∵A(﹣m,0),B(3m,0),m>0,
∴ ,圆的半径为
,圆的半径为 AB=2m。
AB=2m。
∴OM=AM﹣OA=2m﹣m=m。
∴抛物线的顶点P的坐标为:(m,﹣2m)。
∵二次函数 (m>0)的顶点P的坐标为:(m,﹣4m2),
(m>0)的顶点P的坐标为:(m,﹣4m2),
∴﹣2m=﹣4m2,解得m1= ,m2=0(舍去)。
,m2=0(舍去)。
∴二次函数的解析式为 ,即
,即 。
。
(3)如图,连接CM,

在Rt△OCM中,
∵∠COM=90°,CM=2m=2× =1,OM=m=
=1,OM=m= ,
,
∴ 。
。
∴CD=2OC= 。
。
 ,∴当y=0时,
,∴当y=0时, 。
。解得x1=﹣m,x2=3m。
∵m>0,∴A、B两点的坐标分别是(﹣m,0),(3m,0)。
(2)∵A(﹣m,0),B(3m,0),m>0,
∴
 ,圆的半径为
,圆的半径为 AB=2m。
AB=2m。∴OM=AM﹣OA=2m﹣m=m。
∴抛物线的顶点P的坐标为:(m,﹣2m)。
∵二次函数
 (m>0)的顶点P的坐标为:(m,﹣4m2),
(m>0)的顶点P的坐标为:(m,﹣4m2),∴﹣2m=﹣4m2,解得m1=
 ,m2=0(舍去)。
,m2=0(舍去)。∴二次函数的解析式为
 ,即
,即 。
。(3)如图,连接CM,

在Rt△OCM中,
∵∠COM=90°,CM=2m=2×
 =1,OM=m=
=1,OM=m= ,
,∴
 。
。∴CD=2OC=
 。
。(1)解关于x的一元二次方程 ,求出x的值,即可得到A、B两点的坐标。
,求出x的值,即可得到A、B两点的坐标。
(2)由二次函数图象的顶点P在以AB为直径的圆上,A、B是抛物线与x轴的交点,根据抛物线的对称性及圆的半径处处相等可知PM是AB的垂直平分线,且MP=MA=MB= AB,得出点P的坐标为(m,﹣2m),又根据二次函数的顶点式为
AB,得出点P的坐标为(m,﹣2m),又根据二次函数的顶点式为 (m>0),得出顶点P的坐标为:(m,﹣4m2),则﹣2m=﹣4m2,解方程求出m的值,再把m的值代入
(m>0),得出顶点P的坐标为:(m,﹣4m2),则﹣2m=﹣4m2,解方程求出m的值,再把m的值代入 ,即可求出二次函数的解析式。
,即可求出二次函数的解析式。
(3)连接CM.根据(2)中的结论,先在Rt△OCM中,求出CM,OM的长度,利用勾股定理列式求出OC的长,再根据垂径定理得出弦CD的长等于OC的2倍。
 ,求出x的值,即可得到A、B两点的坐标。
,求出x的值,即可得到A、B两点的坐标。(2)由二次函数图象的顶点P在以AB为直径的圆上,A、B是抛物线与x轴的交点,根据抛物线的对称性及圆的半径处处相等可知PM是AB的垂直平分线,且MP=MA=MB=
 AB,得出点P的坐标为(m,﹣2m),又根据二次函数的顶点式为
AB,得出点P的坐标为(m,﹣2m),又根据二次函数的顶点式为 (m>0),得出顶点P的坐标为:(m,﹣4m2),则﹣2m=﹣4m2,解方程求出m的值,再把m的值代入
(m>0),得出顶点P的坐标为:(m,﹣4m2),则﹣2m=﹣4m2,解方程求出m的值,再把m的值代入 ,即可求出二次函数的解析式。
,即可求出二次函数的解析式。(3)连接CM.根据(2)中的结论,先在Rt△OCM中,求出CM,OM的长度,利用勾股定理列式求出OC的长,再根据垂径定理得出弦CD的长等于OC的2倍。

练习册系列答案
相关题目
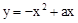 (a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
 ?若存在,请直接写出d3的值;若不存在,请说明理由.
?若存在,请直接写出d3的值;若不存在,请说明理由. 的图象如图所示,则m的值是
的图象如图所示,则m的值是




 (
( 是常数)
是常数) 轴只有一个交点,求
轴只有一个交点,求 在某反比例函数的图像上,要使该反比例函数和二次函数
在某反比例函数的图像上,要使该反比例函数和二次函数 随
随 两点,且
两点,且 ,
, ,在
,在 的图象如图所示,反比例函数
的图象如图所示,反比例函数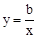 与一次函数
与一次函数 在同一平面直角坐标系中的大致图象是
在同一平面直角坐标系中的大致图象是

 1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:
1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论: ;④3≤n≤4中,
;④3≤n≤4中,