题目内容
【题目】观察下列两个等式：
，
，给出定义如下：我们称使等式 
成立的一对有理数
，
为“共生有理数对”，记为（，），如：数对（
，
），（
，
），都是“共生有理数对”．
（1）数对（
，
），（
，
）中是“共生有理数对”吗？说明理由．
（2）若（
，
）是“共生有理数对”，则（
，
）是“共生有理数对”吗？说明理由．
【答案】(1) (2,1)不是“共生有理数对”，
是“共生有理数对”；理由见详解.
(2) (n,m)是“共生有理数对”， 理由见详解.
【解析】
（1）根据“共生有理数对”的定义即可判断；
（2）根据“共生有理数对”的定义即可判断；
(1)21=3，2×1+1=1，
∴21≠2×1+1，
∴(2,1)不是“共生有理数对”，
∵
∴
∴
是“共生有理数对”；
(2)是.
理由： n (m)=n+m，
n(m)+1=mn+1
∵(m,n)是“共生有理数对”
∴mn=mn+1
∴n+m=mn+1
∴(n,m)是“共生有理数对”，
练习册系列答案
相关题目
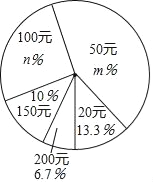
【题目】某中学在一次爱心捐款活动中，全体同学积极踊跃捐款．现抽查了九年级（1）班全班同学捐款情况，并绘制出如下的统计表和统计图：
捐款（元） | 20 | 50 | 100 | 150 | 200 |
人数（人） | 4 | 12 | 9 | 3 | 2 |
求：（Ⅰ）m=_____，n=_____；
（Ⅱ）求学生捐款数目的众数、中位数和平均数；
（Ⅲ）若该校有学生2500人，估计该校学生共捐款多少元？
