题目内容
 一个反比例函数
一个反比例函数 与一次函数y=kx+b的图象有一个交点为A(1,3),一次函数y=kx+b的图象与x轴相交于B,且
与一次函数y=kx+b的图象有一个交点为A(1,3),一次函数y=kx+b的图象与x轴相交于B,且 .
.
(1)求两个函数的解析式;
(2)求两个函数图象另一个交点的坐标;
(3)直接写出不等式 的解集.
的解集.
解:(1)∵点A(1,3)在反比例函数图象上,
∴ =3,
=3,
解得m=3,
∴反比例函数解析式为y= ,
,
∵点A(1,3),
∴OA= =
= ,
,
又∵ =
= ,
,
∴OB=2,
∴点B的坐标为(-2,0),
∴ ,
,
解得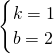 ,
,
∴一次函数解析式为y=x+2;
(2)联立两函数解析式得 ,
,
解得 ,
, ,
,
∴另一交点的坐标为(-3,-1);
(3)不等式可化为kx+b≤ ,
,
结合图形可知,当x≤-3或0<x≤1时,kx+b≤ .
.
分析:(1)把点A的坐标代入反比例函数表达式,求解即可得到反比例函数解析式,利用勾股定理求出OA的长度,然后求出OB的长度,得到点B的坐标,利用待定系数法求解即可得到一此函数解析式;
(2)联立两函数解析式求解即可得到另一交点的坐标;
(3)根据函数图象,写出反比例函数图象在一次函数图象上方的x的取值范围即可.
点评:本题是对反比例函数的综合考查,待定系数法求反比例函数解析式,待定系数法求一次函数解析式,以及另一图形求不等式的解集,联立两函数解析式求交点坐标是常用的方法之一,需熟练掌握并灵活运用.
∴
 =3,
=3,解得m=3,
∴反比例函数解析式为y=
 ,
,∵点A(1,3),
∴OA=
 =
= ,
,又∵
 =
= ,
,∴OB=2,
∴点B的坐标为(-2,0),
∴
 ,
,解得
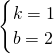 ,
,∴一次函数解析式为y=x+2;
(2)联立两函数解析式得
 ,
,解得
 ,
, ,
,∴另一交点的坐标为(-3,-1);
(3)不等式可化为kx+b≤
 ,
,结合图形可知,当x≤-3或0<x≤1时,kx+b≤
 .
.分析:(1)把点A的坐标代入反比例函数表达式,求解即可得到反比例函数解析式,利用勾股定理求出OA的长度,然后求出OB的长度,得到点B的坐标,利用待定系数法求解即可得到一此函数解析式;
(2)联立两函数解析式求解即可得到另一交点的坐标;
(3)根据函数图象,写出反比例函数图象在一次函数图象上方的x的取值范围即可.
点评:本题是对反比例函数的综合考查,待定系数法求反比例函数解析式,待定系数法求一次函数解析式,以及另一图形求不等式的解集,联立两函数解析式求交点坐标是常用的方法之一,需熟练掌握并灵活运用.

练习册系列答案
相关题目
“相约红色重庆,共享绿色园博”,位于重庆市北部新区的国际园林博览会是一个集自然景观和人文景观为一体的大型城市生态公园.自2011年11月19日开园以来,某商家在园博园内出售纪念品“山娃”玩偶.十周以来,该纪念品深受游人喜爱,其销售量不断增加,销售量y(件)与周数x(1≤x≤10,且x取整数)之间所满足的函数关系如下表所示:
| 周数x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 销售量y(件) | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y与x之间的函数关系式;根据题意,直接写出z与x之间满足的一次函数关系式;
(2)求前十周哪一周的销售利润最大,并求出此最大利润;
(3)从十一周开始,其他商家陆续入驻园博园,因此该商店的销售情况不如从前.该纪念品的销售量比十周下降a%(0<a<10),于是该商家将此纪念品的销售单价在十周的基础上提高1.4a%.另外,随着园博园管理措施的逐步完善,该商家需每周交纳200元的各种费用.这样,十一周的销售利润恰好与十周持平.请参考以下数据,估算出a的整数值.
(参考数据:222=484,232=529,242=576,252=625)
“相约红色重庆,共享绿色园博”,位于重庆市北部新区的国际园林博览会是一个集自然景观和人文景观为一体的大型城市生态公园.自2011年11月19日开园以来,某商家在园博园内出售纪念品“山娃”玩偶.十周以来,该纪念品深受游人喜爱,其销售量不断增加,销售量y(件)与周数x(1≤x≤10,且x取整数)之间所满足的函数关系如下表所示:
为回馈顾客,该商家将此纪念品的价格不断下调,其销售单价z(元)与周数x(1≤x≤10,且x取整数)之间成一次函数关系,且第一周的销售单价为68元,第二周的销售单价为66元.另外,已知该纪念品每件的成本为30元.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y与x之间的函数关系式;根据题意,直接写出z与x之间满足的一次函数关系式;
(2)求前十周哪一周的销售利润最大,并求出此最大利润;
(3)从十一周开始,其他商家陆续入驻园博园,因此该商店的销售情况不如从前.该纪念品的销售量比十周下降a%(0<a<10),于是该商家将此纪念品的销售单价在十周的基础上提高1.4a%.另外,随着园博园管理措施的逐步完善,该商家需每周交纳200元的各种费用.这样,十一周的销售利润恰好与十周持平.请参考以下数据,估算出a的整数值.
(参考数据:222=484,232=529,242=576,252=625)
| 周数x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 销售量y(件) | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y与x之间的函数关系式;根据题意,直接写出z与x之间满足的一次函数关系式;
(2)求前十周哪一周的销售利润最大,并求出此最大利润;
(3)从十一周开始,其他商家陆续入驻园博园,因此该商店的销售情况不如从前.该纪念品的销售量比十周下降a%(0<a<10),于是该商家将此纪念品的销售单价在十周的基础上提高1.4a%.另外,随着园博园管理措施的逐步完善,该商家需每周交纳200元的各种费用.这样,十一周的销售利润恰好与十周持平.请参考以下数据,估算出a的整数值.
(参考数据:222=484,232=529,242=576,252=625)
“相约红色重庆,共享绿色园博”,位于重庆市北部新区的国际园林博览会是一个集自然景观和人文景观为一体的大型城市生态公园.自2011年11月19日开园以来,某商家在园博园内出售纪念品“山娃”玩偶.十周以来,该纪念品深受游人喜爱,其销售量不断增加,销售量y(件)与周数x(1≤x≤10,且x取整数)之间所满足的函数关系如下表所示:
为回馈顾客,该商家将此纪念品的价格不断下调,其销售单价z(元)与周数x(1≤x≤10,且x取整数)之间成一次函数关系,且第一周的销售单价为68元,第二周的销售单价为66元.另外,已知该纪念品每件的成本为30元.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y与x之间的函数关系式;根据题意,直接写出z与x之间满足的一次函数关系式;
(2)求前十周哪一周的销售利润最大,并求出此最大利润;
(3)从十一周开始,其他商家陆续入驻园博园,因此该商店的销售情况不如从前.该纪念品的销售量比十周下降a%(0<a<10),于是该商家将此纪念品的销售单价在十周的基础上提高1.4a%.另外,随着园博园管理措施的逐步完善,该商家需每周交纳200元的各种费用.这样,十一周的销售利润恰好与十周持平.请参考以下数据,估算出a的整数值.
(参考数据:222=484,232=529,242=576,252=625)
| 周数x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 销售量y(件) | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y与x之间的函数关系式;根据题意,直接写出z与x之间满足的一次函数关系式;
(2)求前十周哪一周的销售利润最大,并求出此最大利润;
(3)从十一周开始,其他商家陆续入驻园博园,因此该商店的销售情况不如从前.该纪念品的销售量比十周下降a%(0<a<10),于是该商家将此纪念品的销售单价在十周的基础上提高1.4a%.另外,随着园博园管理措施的逐步完善,该商家需每周交纳200元的各种费用.这样,十一周的销售利润恰好与十周持平.请参考以下数据,估算出a的整数值.
(参考数据:222=484,232=529,242=576,252=625)