Question

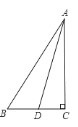
【题目】△ABC中，∠C=90°，∠BAC的平分线交BC于D，且CD=15，AC=30，则AB的长为（ ）

A. 30 B. 40 C. 50 D. 60

Answer 1

【答案】C

【解析】

作DE⊥AB，易得△ABC∽△DBE，则，设BD=x，BE=y，则，解得x=2y-15，在Rt△DBE中，BD2=DE2+BE2，即（2y-15）2=y2+152，求得y的值，即可求得AB．

如图，作DE⊥AB，

∴∠BED=90°，

∴∠BED=∠C=90°，

∵∠EBD=∠ABC，

∴△ABC∽△DBE，

∴，

设BD=x，BE=y，则，

30y=152+15x，

x=2y-15，

在Rt△DBE中，BD2=DE2+BE2，

即（2y-15）2=y2+152，

y（y-20）=0，

∴y=20，

AB=AE+BE=30+20=50．

故选C．