题目内容
国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价y1(万元)之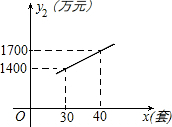 间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.(1)求出y2与x之间的函数关系式并直接写出x的取值范围;
(2)当月产量x(套)为多少时,利润为1900万元?
(3)求出月利润的范围.
分析:(1)设函数关系式为y2=kx+b,把(30,1400)(40,1700)代入求解即可;
(2)根据利润=售价-成本列出关系式,进而解答即可.
(3)得出函数关系式,然后根据二次函数的最大值及最小值可确定答案.
(2)根据利润=售价-成本列出关系式,进而解答即可.
(3)得出函数关系式,然后根据二次函数的最大值及最小值可确定答案.
解答:解:(1)设函数关系式为y2=kx+b,把坐标(30,1400)(40,1700)代入,
解得:
∴函数关系式y2=30x+500(25≤x≤40);
(2)1900=x[170-2x-(30x+500)],
解得:x=30或40.
∴x=30或40时,利润为1900万元;
(3)设月利润为w万元,则w=-2(x-35)2+1950,因为对称轴是x=35,
由对称性可知,当x=25时,w最小=1750,
因为顶点坐标为(35,1950),
所以w最大=1950,所以1750≤w≤1950.
|
解得:
|
∴函数关系式y2=30x+500(25≤x≤40);
(2)1900=x[170-2x-(30x+500)],
解得:x=30或40.
∴x=30或40时,利润为1900万元;
(3)设月利润为w万元,则w=-2(x-35)2+1950,因为对称轴是x=35,
由对称性可知,当x=25时,w最小=1750,
因为顶点坐标为(35,1950),
所以w最大=1950,所以1750≤w≤1950.
点评:本题考查了函数关系式及其最大值的求解,同时还有自变量取值范围的求解,有一定难度,注意利用二次函数的最值进行函数范围的确定.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
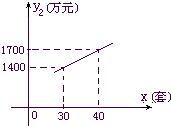 间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.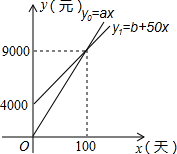 (2012•泉州)国家推行“节能减排,低碳经济”政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时x(单位:天)之间分别满足关系式:y0=ax、y1=b+50x,如图所示.
(2012•泉州)国家推行“节能减排,低碳经济”政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时x(单位:天)之间分别满足关系式:y0=ax、y1=b+50x,如图所示.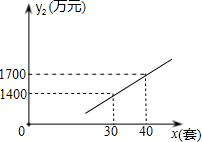 合适?
合适?