题目内容
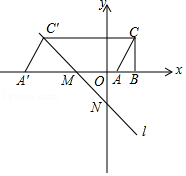
【题目】如图，直线l与x轴，y轴分别交于M，N两点，且OM=ON=3．
（1）求这条直线的函数表达式；
（2）Rt△ABC与直线l在同一个平面直角坐标系内，其中∠ABC=90°，AC=2 
，A（1，0），B（3，0），将△ABC沿着x轴向左平移，当点C落在直线l上时，求线段AC扫过的面积．
【答案】
（1）
解：设该直线的函数表达式为y=kx+b（k≠0），
∵OM=ON=3，且M、N分别在x轴负半轴、y轴负半轴上，
∴M（﹣3，0），N（0，﹣3）．
将M（﹣3，0）、N（0，﹣3）代入y=kx+b，
，解得： 
，
∴这条直线的函数表达式为y=﹣x﹣3．
（2）
解：∵A（1，0），B（3，0），
∴AB=2．
∵∠ABC=90°，AC=2 
，
∴BC=4，
∴C（3，4）．
设平移后点A、C的对应点分别为A′、C′，
当y=﹣x﹣3=4时，x=﹣7，
∴C′（﹣7，4），
∴CC′=10．
∵线段AC扫过的四边形ACC′A′为平行四边形，
∴S=CC′BC=10×4=40．
答：线段AC扫过的面积为40．
【解析】（1）根据OM=ON=3结合图形可得出点M、N的坐标，由点M、N的坐标利用待定系数法即可求出直线MN的函数表达式；（2）通过解直角三角形可得出点C的坐标，设平移后点A、C的对应点分别为A′、C′，利用一次函数图象上点的坐标特征可找出点C′的坐标，根据平移的性质结合平行四边形的面积公式即可求出线段AC扫过的面积．
练习册系列答案
相关题目
