题目内容
已知点E在矩形ABCD边CD上，将矩形沿AE折叠后点D落在点D′，∠CED′=55°，则∠BAD′的大小是（ ）
| A、30° | B、35° |
| C、45° | D、60° |
考点：翻折变换（折叠问题）
专题：
分析：利用平角定义及翻折前后对应角相等易得∠D′EA度数，进而利用三角形内角和定理可求得∠EAD′度数，利用翻折前后对应角相等和三个角的和为90°可得所求的角的度数．
解答：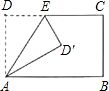
解：将矩形ABCD沿AE折叠，得到△ADE≌△ADE′，
∴∠EAD′=
∠DAD′，∠D′EA=
∠D′ED，
∵∠CED′=55°，
∴∠D′EA=（180°-∠CED′）÷2=62.5°，
∴∠D′AE=90°-∠D′EA=90°-62.5°=27.5°，
∴∠BAD′=90°-2∠EAD′=90°-55°=35°．
故选B．
解：将矩形ABCD沿AE折叠，得到△ADE≌△ADE′，∴∠EAD′=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠CED′=55°，
∴∠D′EA=（180°-∠CED′）÷2=62.5°，
∴∠D′AE=90°-∠D′EA=90°-62.5°=27.5°，
∴∠BAD′=90°-2∠EAD′=90°-55°=35°．
故选B．
点评：本题主要考查翻折变换的性质、正方形的性质、四边形内角和定理，解题的关键在于求出∠DAD′的度数．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、底角相等的两个等腰三角形全等 |
| B、等腰三角形的中线、高、角平分线互相重合 |
| C、“同位角相等”是一个命题 |
| D、在同一个三角形中，有两个底角相等的三角形是等腰三角形 |
如图，在长方形纸片ABCD中，AD=4cm，AB=8cm，按如图方式折叠，使点B与点D重合，折痕为EF，则DE=
有下列说法：①任何无理数都是无限小数；②数轴上的点与有理数一一对应；③绝对值等于本身的数是0；④0除以任何数都得0；⑤一个数的平方根等于它本身的数是0，1．其中正确的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
下列判断正确的是（ ）
| A、锐角的补角不一定是钝角 |
| B、一个角的补角一定大于这个角 |
| C、如果两个角是同一个角的补角，那么它们相等 |
| D、锐角和钝角互补 |