题目内容
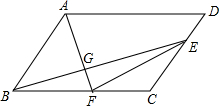 如图,四边形ABCD为平行四边形,DE:EC=1:2,F是BC的中点,AF交BE于G点,则:
如图,四边形ABCD为平行四边形,DE:EC=1:2,F是BC的中点,AF交BE于G点,则:
①△EBF与△EFC面积相等,
②△BEC的面积是平行四边形ABCD面积的 ,
,
③△ABF的面积是平行四边形ABCD面积的 ,
,
④△BFG的面积是△BGA面积的 .
.
以上结论正确的是________.
①③④
分析:①由F是BC的中点,根据等底等高的三角形的面积相等,即可求得答案;
②首先连接BD,易得△BEC的面积是△BCD的面积的 ,且△BCD与△ABD面积相等,继而求得答案;
,且△BCD与△ABD面积相等,继而求得答案;
③首先连接AC,由△ABF的面积是△ABC的面积的 ,且△ABC与△ADC面积相等,即可求得答案;
,且△ABC与△ADC面积相等,即可求得答案;
④首先取线段BE的中点H,连接FH,易得FH:AB=1:3,继而求得答案.
解答: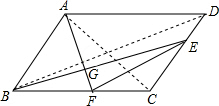 解:①∵F是BC的中点,
解:①∵F是BC的中点,
∴△EBF与△EFC面积相等,
故正确;
②连接BD,
∵DE:EC=1:2,
∴△BEC的面积是△BCD的面积的 ,且△BCD与△ABD面积相等,
,且△BCD与△ABD面积相等,
∴△BEC的面积是平行四边形ABCD面积的 ;
;
故错误;
③连接AC,
∵F是BC的中点,
∴△ABF的面积是△ABC的面积的 ,且△ABC与△ADC面积相等,
,且△ABC与△ADC面积相等,
∴△ABF的面积是平行四边形ABCD面积的 ;
;
故正确;
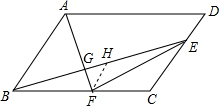 ④取线段BE的中点H,连接FH,
④取线段BE的中点H,连接FH,
∵F是BC的中点,
∴FH∥CD,FH= CE,
CE,
∴FH= AB,
AB,
∵AB∥CD,
∴FH∥AB,
∴△FGH∽△AGB,
∴FG:AG=FH:AB=1:3,
∴△BFG的面积是△BGA面积的 .
.
故④正确.
故答案为:①③④.
点评:此题考查了平行四边形的性质、相似三角形的判定与性质以及三角形的中位线的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
分析:①由F是BC的中点,根据等底等高的三角形的面积相等,即可求得答案;
②首先连接BD,易得△BEC的面积是△BCD的面积的
 ,且△BCD与△ABD面积相等,继而求得答案;
,且△BCD与△ABD面积相等,继而求得答案;③首先连接AC,由△ABF的面积是△ABC的面积的
 ,且△ABC与△ADC面积相等,即可求得答案;
,且△ABC与△ADC面积相等,即可求得答案;④首先取线段BE的中点H,连接FH,易得FH:AB=1:3,继而求得答案.
解答:
 解:①∵F是BC的中点,
解:①∵F是BC的中点,∴△EBF与△EFC面积相等,
故正确;
②连接BD,
∵DE:EC=1:2,
∴△BEC的面积是△BCD的面积的
 ,且△BCD与△ABD面积相等,
,且△BCD与△ABD面积相等,∴△BEC的面积是平行四边形ABCD面积的
 ;
;故错误;
③连接AC,
∵F是BC的中点,
∴△ABF的面积是△ABC的面积的
 ,且△ABC与△ADC面积相等,
,且△ABC与△ADC面积相等,∴△ABF的面积是平行四边形ABCD面积的
 ;
;故正确;
 ④取线段BE的中点H,连接FH,
④取线段BE的中点H,连接FH,∵F是BC的中点,
∴FH∥CD,FH=
 CE,
CE,∴FH=
 AB,
AB,∵AB∥CD,
∴FH∥AB,
∴△FGH∽△AGB,
∴FG:AG=FH:AB=1:3,
∴△BFG的面积是△BGA面积的
 .
.故④正确.
故答案为:①③④.
点评:此题考查了平行四边形的性质、相似三角形的判定与性质以及三角形的中位线的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.