Question

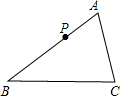已知：在△ABC中，P是AB上一点，连接 CP，当满足条件：∠ACP=________或∠APC=________或 AC²=________时，△ACP∽△ABC．

Answer 1

∠ABC    ∠ACB    AP•AB
分析：连接PC，由图可得，两三角形已有一组角（公共角）对应相等，再加一组角对应相等或两组对应边的比相等且夹角对应相等的两个三角形相似，有此填空即可．
解答：证明：连接PC，
∵∠A=∠A，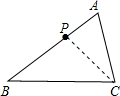
∴当∠ACP=∠ABC或∠APC=∠ACB，或（AC²=AP•BP）时，△ACP∽△ABC，
故答案为：∠ABC；∠ACB；AP•AB．
点评：本题考查了相似三角形的判定：根据相似三角形的判定方法（1）三边法：三组对应边的比相等的两个三角形相似；（2）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；（3）两角法：有两组角对应相等的两个三角形相似．