题目内容
解方程组：
．
解：把x+y=7两边平方，得
x2+y2+2xy=49
把上式与x2+y2=25相减，化简得：xy=12，
∴x、y是方程a2-7a+12=0的解，
解方程a2-7a+12=0，得a1=3，a2=4，
∴原方程的解为：
或
．
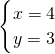分析：把x+y=7两边平方后得到：x2+y2+2xy=49，与第一个方程相减后得到：xy=12，故根据一元二次方程的根与系数的关系构造新的一元二次方程，求得该方程的解，即为原方程的解．
点评：本题通过对原方程组中的方程变形后，根据一元二次方程的根与系数的关系建立新的方程，进而求得原方程的解，利用了转化思想．
x2+y2+2xy=49
把上式与x2+y2=25相减，化简得：xy=12，
∴x、y是方程a2-7a+12=0的解，
解方程a2-7a+12=0，得a1=3，a2=4，
∴原方程的解为：
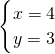或．分析：把x+y=7两边平方后得到：x2+y2+2xy=49，与第一个方程相减后得到：xy=12，故根据一元二次方程的根与系数的关系构造新的一元二次方程，求得该方程的解，即为原方程的解．
点评：本题通过对原方程组中的方程变形后，根据一元二次方程的根与系数的关系建立新的方程，进而求得原方程的解，利用了转化思想．
练习册系列答案
步步高达标卷系列答案
相关题目
（1）解方程组：