题目内容
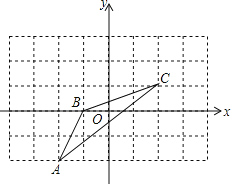
【题目】如图,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,图象与
,图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.

![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 设抛物线对称轴与直线
设抛物线对称轴与直线![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
![]() 点
点![]() 为直线
为直线![]() 上的任意一点,过点
上的任意一点,过点![]() 作
作![]() 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点![]() ,问是否存在点
,问是否存在点![]() 使
使![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)2;(3)见解析.
;(2)2;(3)见解析.
【解析】
(1)可设抛物线解析式为顶点式,把C点坐标代入可求得抛物线解析式;
(2)由抛物线解析式可求得A、B坐标,利用待定系数法可求得直线BC解析式,利用对称轴可求得D点坐标,则可求得AD2、AC2和CD2,利用勾股定理的逆定理可判定△ACD为直角三角形,则可求得其面积;
(3)根据题意可分∠DFE=90°和∠EDF=90°两种情况,当∠DFE=90°时,可知DF∥x轴,则可求得E点纵坐标,代入抛物线解析式可求得E点坐标;当∠EDF=90°时,可求得直线AD解析式,联立直线AC和抛物线解析式可求得点E的横坐标,代入直线BC可求得点E的坐标.
解:![]() ∵抛物线的顶点坐标为
∵抛物线的顶点坐标为![]() ,
,
∴可设抛物线解析式为![]() ,
,
把![]() 代入可得
代入可得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为![]() ;
;
![]() 在
在![]() 中,令
中,令![]() 可得
可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴![]() ,
,![]() ,
,
设直线![]() 解析式为
解析式为![]() ,把
,把![]() 代入得:
代入得:![]() ,解得
,解得![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
由![]() 可知抛物线的对称轴为
可知抛物线的对称轴为![]() ,此时
,此时![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() 是以
是以![]() 为斜边的直角三角形,
为斜边的直角三角形,
∴![]() ;
;
![]() 由题意知
由题意知![]() 轴,则
轴,则![]() ,
,
∴![]() 为直角三角形,分
为直角三角形,分![]() 和
和![]() 两种情况,
两种情况,
①当![]() 时,即
时,即![]() 轴,则
轴,则![]() 、
、![]() 的纵坐标相同,
的纵坐标相同,
∴![]() 点纵坐标为
点纵坐标为![]() ,
,
∵点![]() 在抛物线上,
在抛物线上,
∴![]() ,解得
,解得![]() ,即点
,即点![]() 的横坐标为
的横坐标为![]() ,
,
∵点![]() 在直线
在直线![]() 上,
上,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
②当![]() 时,
时,
∵![]() ,
,![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
∵直线![]() 解析式为
解析式为![]() ,
,
∴![]() ,
,
∴直线![]() 与抛物线的交点即为
与抛物线的交点即为![]() 点,
点,
联立直线![]() 与抛物线解析式有
与抛物线解析式有![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 点坐标为
点坐标为![]() 或
或![]() ,
,
综上可知存在满足条件的点![]() ,其坐标为
,其坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目