题目内容
如图,点D、E在△ABC的边BC上,AB=AC,AD=AE,且BD=4,求EC的长.
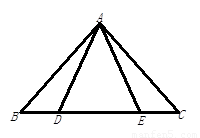
【答案】
4
【解析】
试题分析:直观上看BD=CE,证明线段相等的方法一般是全等,包含BD和CE的两个三角形是△ABD和△AEC,找两个三角形全等的条件,因为AB=AC,所以∠B=∠C,又因为AD=AE,所以∠ADE=∠AED,即∠ADB=∠AEC,在△ABD和△AEC中,∠B=∠C,∠ADB=∠AEC,AB=AC,所以△ABD≌△AEC(AAS),所以EC=BD=4.
试题解析:∵AB=AC,
∴∠B=∠C,
又∵AD=AE,
∴∠ADE=∠AED,即∠ADB=∠AEC,
在△ABD和△AEC中, ∠B=∠C, ∠ADB=∠AEC, AB=AC,
∴△ABD≌△AEC(AAS),
∴EC=BD=4.
考点:三角形的全等.

练习册系列答案
相关题目


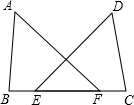 如图,点E、F在BC上,AB=DC,∠B=∠C,∠A=∠D,
如图,点E、F在BC上,AB=DC,∠B=∠C,∠A=∠D,
 如图,点C、D在线段AB上,且C为AB的一个四等分点,D为AC中点,若BC=2,则BD的长为
如图,点C、D在线段AB上,且C为AB的一个四等分点,D为AC中点,若BC=2,则BD的长为