题目内容
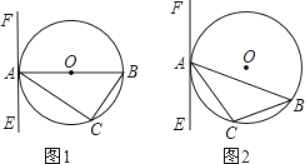
【题目】如图，点I和O分别是△ABC的内心和外心，则∠AIB和∠AOB的关系为（ ）
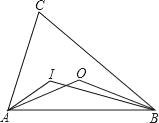
A. ∠AIB＝∠AOBB. ∠AIB≠∠AOB
C. 2∠AIB﹣
∠AOB＝180°D. 2∠AOB﹣∠AIB＝180°
【答案】C
【解析】
根据圆周角定义，以及内心的定义，可以利用∠C表示出∠AIB和∠AOB，即可得到两个角的关系．
解：∵点O是△ABC的外心，
∴∠AOB＝2∠C，
∴∠C＝
∠AOB，
∵点I是△ABC的内心，
∴∠IAB＝∠CAB，∠IBA＝∠CBA，
∴∠AIB＝180°﹣（∠IAB+∠IBA）
＝180°﹣（∠CAB+∠CBA），
＝180°﹣（180°﹣∠C）
＝90°+∠C，
∴2∠AIB＝180°+∠C，
∵∠AOB＝2∠C，
∴∠AIB＝90°+∠AOB，即2∠AIB﹣∠AOB＝180°．
故选：C．
练习册系列答案
全能测控期末小状元系列答案
相关题目
