题目内容
如图所示,直线 与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.(1)求证:MC⊥OA;
(2)求直线BC的解析式.

【答案】分析:(1)由∠COD=∠OBC,可以得出 ,再利用垂径定理就可以直接得出结论MC⊥OA;
,再利用垂径定理就可以直接得出结论MC⊥OA;
(2)由直线的解析式可以求出OA、OB的值,由(1)的结论就可以求出OG、GM的值,连接OM求出⊙M的半径,从而求出GC的值而求出C点的坐标,最后利用待定系数法就可以求出直线BC的解析式.
解答:(1)证明:∵∠COD=∠OBC,
∴ ,
,
∵点M是圆心,
∴由垂径定理的推论,得
MC⊥OA;
(2)解:∵MC⊥OA,
∴OG=GA= OA,
OA,
∵点M是圆心,
∴BM=AM,
∴GM是△AOB的中位线,
∴GM= OB,
OB,
∵ 与x轴、y轴分别交于A、B两点,
与x轴、y轴分别交于A、B两点,
∴当x=0时,y= ,
,
当y=0时,x=3,
∴B(0, ),A(3,0)
),A(3,0)
∴OB= ,OA=3,
,OA=3,
∴MG= ,OG=
,OG= ,连接OM,在Rt△OGM中,由勾股定理,得
,连接OM,在Rt△OGM中,由勾股定理,得
OM= ,
,
∴GC= -
- =
= ,
,
∵点C在第三象限,
∴C( ,-
,- ).
).
设直线BC的解析式为:y=kx+b,
∴ 解得:
解得: ,
,
直线BC的解析式为:y=- x+
x+
点评:本题是一道一次函数的综合试题,考查了一次函数的图象上点的坐标的特征,待定系数法求一次函数的解析式,三角形中位线的性质的运用,勾股定理的运用及圆的相关性质的运用.
 ,再利用垂径定理就可以直接得出结论MC⊥OA;
,再利用垂径定理就可以直接得出结论MC⊥OA;(2)由直线的解析式可以求出OA、OB的值,由(1)的结论就可以求出OG、GM的值,连接OM求出⊙M的半径,从而求出GC的值而求出C点的坐标,最后利用待定系数法就可以求出直线BC的解析式.
解答:(1)证明:∵∠COD=∠OBC,
∴
 ,
,∵点M是圆心,
∴由垂径定理的推论,得
MC⊥OA;
(2)解:∵MC⊥OA,
∴OG=GA=
 OA,
OA,∵点M是圆心,
∴BM=AM,
∴GM是△AOB的中位线,
∴GM=
 OB,
OB,∵
 与x轴、y轴分别交于A、B两点,
与x轴、y轴分别交于A、B两点,
∴当x=0时,y=
 ,
,当y=0时,x=3,
∴B(0,
 ),A(3,0)
),A(3,0)∴OB=
 ,OA=3,
,OA=3,∴MG=
 ,OG=
,OG= ,连接OM,在Rt△OGM中,由勾股定理,得
,连接OM,在Rt△OGM中,由勾股定理,得OM=
 ,
,∴GC=
 -
- =
= ,
,∵点C在第三象限,
∴C(
 ,-
,- ).
).设直线BC的解析式为:y=kx+b,
∴
 解得:
解得: ,
,直线BC的解析式为:y=-
 x+
x+
点评:本题是一道一次函数的综合试题,考查了一次函数的图象上点的坐标的特征,待定系数法求一次函数的解析式,三角形中位线的性质的运用,勾股定理的运用及圆的相关性质的运用.

练习册系列答案
相关题目
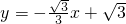 与x轴、y轴分别交于A、B两点,直线BC交x轴于D,
与x轴、y轴分别交于A、B两点,直线BC交x轴于D, 交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
交△ABO的外接圆⊙M于C,已知∠COD=∠OBC. 与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
 与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
 与y轴交于点
与y轴交于点 ,以
,以 为边作正方形
为边作正方形 然后
然后 与直线
与直线 ,得到第一个梯形
,得到第一个梯形 ;再以
;再以 为边作正方形
为边作正方形 ,同样延长
,同样延长 与直线
与直线 得到第二个梯形
得到第二个梯形 ;,再以
;,再以 为边作正方形
为边作正方形 ,延长
,延长 ,得到第三个梯形;……则第2个梯形
,得到第三个梯形;……则第2个梯形
 (n是正整数)个梯形的面积是
(用含n的式子
(n是正整数)个梯形的面积是
(用含n的式子