题目内容
小明在学习二次函数时，总结了如下规律：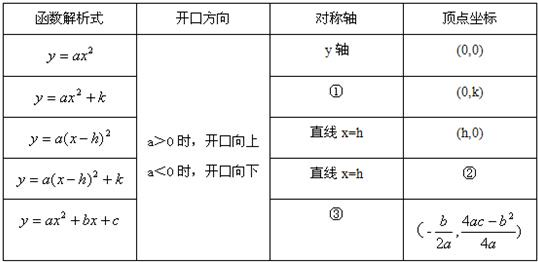
（1）请帮助小明补全此表①
（2）根据此表判断，如何将抛物线y=-2x2经过适当的平移得到抛物线y=-2x2+4x+1．
分析：（1）函数对称轴和顶点坐标的判断，可以先将函数化为顶点坐标再判断，也可用固定公式代入得到；
（2）应先将y=-2x2+4x+1化为完全平方式，即顶点坐标式，再根据左右平移、上下平移y=-2x2得到．
（2）应先将y=-2x2+4x+1化为完全平方式，即顶点坐标式，再根据左右平移、上下平移y=-2x2得到．
解答：解：（1）y轴、（h，k）、直线x=-
；
（2）y=-2x2+4x+1，变形得：y=-2（x-1）2+3，
y=-2x2先向右平移1个单位，再向上平移3个单位得到y=-2x2+4x-1．
| b |
| 2a |
（2）y=-2x2+4x+1，变形得：y=-2（x-1）2+3，
y=-2x2先向右平移1个单位，再向上平移3个单位得到y=-2x2+4x-1．
点评：本题考查了二次函数的性质及函数图象的平移，应注意掌握其平移规律．
练习册系列答案
相关题目
阅读下面的材料：
小明在学习二次函数时，总结了如下规律：
| 函数解析式 | 开口方向 | 对称轴 | 顶点坐标 |
|
| a＞0时，开口向上 a＜0时，开口向下 | y轴 | (0,0) |
|
| ① | (0,k) | |
|
| 直线x=h | (h,0) | |
|
| 直线x=h | ② | |
|
| ③ |
|
(1)请帮助小明补全此表① ② ③
（2）根据此表判断，如何将抛物线
经过适当的平移得到抛物线
.
