题目内容
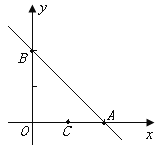
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴交点分别为
轴交点分别为![]() 、
、![]() ,另一直线
,另一直线![]()
![]() 经过
经过![]() ,且把
,且把![]() 分成两部分.
分成两部分.
(1)若![]() 被分成的两部分面积相等,求
被分成的两部分面积相等,求![]() 和
和![]() 的值.
的值.
(2)若![]() 被分成的两部分面积之比为
被分成的两部分面积之比为![]() ,求
,求![]() 和
和![]() 的值.
的值.
【答案】(1)k=-2,b=2;(2) 或
或![]()
【解析】
(1)△AOB被分成的两部分面积相等,那么被分成的两部分都应该是三角形AOB的面积的一半,那么直线y=kx+b(k≠0)必过B点,因此根据B,C两点的函数关系式可得出,直线的函数式.
(2)若△AOB被分成的两部分面积比为1:5,那么被分成的两部分中小三角形的面积就应该是大三角形面积的![]() ,已知了直线过C点,则小三角形的底边是大三角形的OA边的一半,故小三角形的高应该是OB的
,已知了直线过C点,则小三角形的底边是大三角形的OA边的一半,故小三角形的高应该是OB的![]() ,即直线经过的这点的纵坐标应该是
,即直线经过的这点的纵坐标应该是![]() .那么这点应该在y轴和AB上,可分这两种情况进行计算,运用待定系数法求函数的解析式.
.那么这点应该在y轴和AB上,可分这两种情况进行计算,运用待定系数法求函数的解析式.
(1)由题意知:直线y=kx+b(k≠0)必过C点,
∵C是OA的中点,
∴直线y=kx+b一定经过点B,C,如图(1)所示,
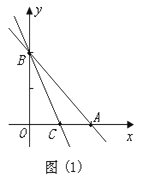
把B,C的坐标代入可得:
![]() ,
,
解得k=2,b=2;
(2)∵S△AOB=12×2×2=2,
∵△AOB被分成的两部分面积比为1:5,那么直线y=kx+b(k≠0)与y轴或AB交点的纵坐标就应该是:2×2×![]() =
=![]() ,
,
①当y=kx+b(k≠0)与直线y=x+2相交时,交点为D,如图(2)所示,

当y=![]() 时,直线y=x+2与y=kx+b(k≠0)的交点D的横坐标就应该是x+2=
时,直线y=x+2与y=kx+b(k≠0)的交点D的横坐标就应该是x+2=![]() ,
,
∴x=![]() ,
,
即交点D的坐标为(![]() ,
,![]() ),
),
又根据C点的坐标为(1,0),可得:

∴k=2,b=2,
②当y=kx+b(k≠0)与y轴相交时,交点为E,如图(3)所示,

∴交点E的坐标就应该是(0,![]() ),又有C点的坐标(1,0),可得:
),又有C点的坐标(1,0),可得:

∴
k=![]() ,b=
,b=![]() ,
,
因此:k=2,b=2或k=![]() ,b=
,b=![]() .
.

练习册系列答案
相关题目