题目内容
计算
(1)一个等腰三角形的一边长为8cm,周长为20cm.求:其它两边的长.
(2)一个多边形的内角和为1800°,并且这个多边形的各个内角都相等,求:这个多边形每一个内角的度数.
(1)一个等腰三角形的一边长为8cm,周长为20cm.求:其它两边的长.
(2)一个多边形的内角和为1800°,并且这个多边形的各个内角都相等,求:这个多边形每一个内角的度数.
分析:(1)已知条件中,本题没有明确说明已知的边长是否是腰长,所以有两种情况讨论,还应判定能否组成三角形.
(2)先根据多边形的内角和公式(n-2)•180°求出多边形的边数,然后利用内角和除以边数即可;
(2)先根据多边形的内角和公式(n-2)•180°求出多边形的边数,然后利用内角和除以边数即可;
解答:解:(1)①底边长为8,则腰长为:(20-8)÷2=6,所以另两边的长为6cm,6cm,能构成三角形;
②腰长为8,则底边长为:20-8×2=4,底边长为8cm,另一个腰长为4cm,能构成三角形.
因此另两边长为8cm、4cm或6cm、6cm.
(2)解:设多边形的边数为n,
则(n-2)•180°=1800°,
解得n=12,
1800°÷12=150°.
这个多边形的每一个内角都等于150°.
②腰长为8,则底边长为:20-8×2=4,底边长为8cm,另一个腰长为4cm,能构成三角形.
因此另两边长为8cm、4cm或6cm、6cm.
(2)解:设多边形的边数为n,
则(n-2)•180°=1800°,
解得n=12,
1800°÷12=150°.
这个多边形的每一个内角都等于150°.
点评:本题考查了多边形的内角与外角及等腰三角形的性质,熟记内角和公式求出多边形的边数是解题的关键.

练习册系列答案
相关题目
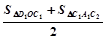 ,S右2=
,S右2=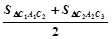 ).
).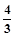 .若存在,请求出点P的坐标;若不存在,请说明理由.
.若存在,请求出点P的坐标;若不存在,请说明理由.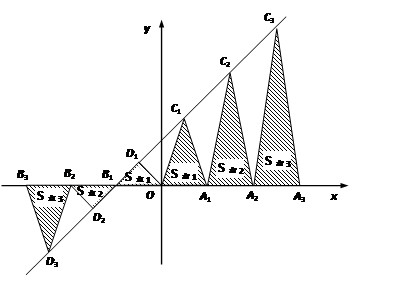
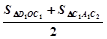 ,S右2=
,S右2=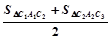 ).
).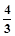 .若存在,请求出点P的坐标;若不存在,请说明理由.
.若存在,请求出点P的坐标;若不存在,请说明理由.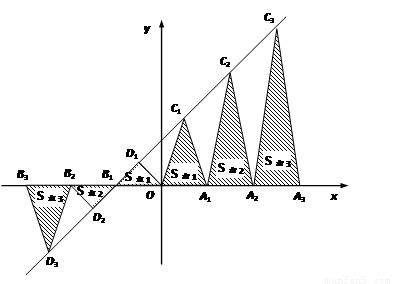
 ; ②
; ② ______
______ ③8+8______
③8+8______
 ;
; ,∴
,∴ ,∴
,∴ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立. ,并指出等号成立时的条件.
,并指出等号成立时的条件.