题目内容
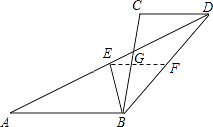
【题目】如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点. 
(1)若BK= ![]() KC,求
KC,求 ![]() 的值;
的值;
(2)连接BE,若BE平分∠ABC,则当AE= ![]() AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=
AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE= ![]() AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
【答案】
(1)解:∵BK= ![]() KC,
KC,
∴ ![]() =
= ![]() ,
,
又∵CD∥AB,
∴△KCD∽△KBA,
∴ ![]() =
= ![]() =
= ![]()
(2)解:当BE平分∠ABC,AE= ![]() AD时,AB=BC+CD;
AD时,AB=BC+CD;
证明:取BD的中点为F,连接EF交BC于G点,
由中位线定理,得EF∥AB∥CD,
∴G为BC的中点,∠GEB=∠EBA,
又∵∠EBA=∠GBE,
∴∠GEB=∠GBE,
∴EG=BG= ![]() BC,而GF=
BC,而GF= ![]() CD,EF=
CD,EF= ![]() AB,
AB,
∵EF=EG+GF,
即: ![]() AB=
AB= ![]() BC+
BC+ ![]() CD;
CD;
∴AB=BC+CD;
同理,当AE= ![]() AD(n>2)时,EF∥AB,
AD(n>2)时,EF∥AB,
同理可得: ![]() =
= ![]() ,则BG=
,则BG= ![]() BC,则EG=BG=
BC,则EG=BG= ![]() BC,
BC,
![]() =
= ![]() =
= ![]() ,则GF=
,则GF= ![]() CD,
CD,
![]() =
= ![]() =
= ![]() ,
,
∴ ![]() +
+ ![]() CD=
CD= ![]() AB,
AB,
∴BC+CD=(n﹣1)AB,
故当AE= ![]() AD(n>2)时,BC+CD=(n﹣1)AB.
AD(n>2)时,BC+CD=(n﹣1)AB.
【解析】(1)由已知得 ![]() =
= ![]() ,由CD∥AB可证△KCD∽△KBA,利用
,由CD∥AB可证△KCD∽△KBA,利用 ![]() =
= ![]() 求值;(2)AB=BC+CD.作△ABD的中位线,由中位线定理得EF∥AB∥CD,可知G为BC的中点,由平行线及角平分线性质,得∠GEB=∠EBA=∠GBE,则EG=BG=
求值;(2)AB=BC+CD.作△ABD的中位线,由中位线定理得EF∥AB∥CD,可知G为BC的中点,由平行线及角平分线性质,得∠GEB=∠EBA=∠GBE,则EG=BG= ![]() BC,而GF=
BC,而GF= ![]() CD,EF=
CD,EF= ![]() AB,利用EF=EG+GF求线段AB、BC、CD三者之间的数量关系;当AE=
AB,利用EF=EG+GF求线段AB、BC、CD三者之间的数量关系;当AE= ![]() AD(n>2)时,EG=BG=
AD(n>2)时,EG=BG= ![]() BC,而GF=
BC,而GF= ![]() CD,EF=
CD,EF= ![]() AB,EF=EG+GF可得BC+CD=(n﹣1)AB.
AB,EF=EG+GF可得BC+CD=(n﹣1)AB.
【考点精析】掌握角平分线的性质定理和相似三角形的判定与性质是解答本题的根本,需要知道定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.