题目内容
11．
如图，已知DC平分∠ACB，且∠1=∠B．求证：∠EDC=∠ECD．
分析 由∠1=∠B，得DE∥BC，可推出∠EDC=∠BCD，在由DC平分∠ACB，可得结论．
解答 证明：∵∠1=∠B，
∴DE∥BC，
∴∠EDC=∠BCD，
∵DC平分∠ACB，
∴∠EDC=∠ECD．
点评 本题主要考查了平行线的判定和性质，熟练应用这一性质和判定是解题的关键．
练习册系列答案
相关题目
1．
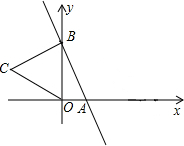如图，直线y=-2x+6与x，y轴分别交于A，B两点，以OB为边在y轴左侧作等边三角形OBC，将点C向右平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为（$\frac{3}{2}$，3）．
如图，直线y=-2x+6与x，y轴分别交于A，B两点，以OB为边在y轴左侧作等边三角形OBC，将点C向右平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为（$\frac{3}{2}$，3）．
2．不等式y+2≤3的正整数解为（ ）
| A． | 1，2 | B． | 2，3 | C． | 2 | D． | 1 |
19．若分式$\frac{x+1}{x-5}$有意义，则x的取值范围是（ ）
| A． | x=1 | B． | x=5 | C． | x≠1 | D． | x≠5 |
3．下列等式是由3x=4x-1根据等式性质变形得到的，其中正确的个数有（ ）
①4x-3x=1；②3x-4x=1；③$\frac{3}{2}x=2x-\frac{1}{2}$；④-1=3x+4x．
①4x-3x=1；②3x-4x=1；③$\frac{3}{2}x=2x-\frac{1}{2}$；④-1=3x+4x．
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
1．如图是一个几何体的三视图，则这个几何体的全面积是（ ）
| A． | 18cm2 | B． | 20cm2 | C． | $（{18+2\sqrt{3}}）$cm2 | D． | $（{18+4\sqrt{3}}）$cm2 |