题目内容
四边形OABC是等腰梯形,OA∥BC,在建立如图所示的平面直角坐标系中,A(4,0),B(3,2),点M从O点出发沿折线段OA-AB以每秒2个单位长的速度向终点 B运动;同时,点N从B点出发沿折线段BC-CO以每秒1个单位长的速度向终点O运动、设运动时间为t秒.
B运动;同时,点N从B点出发沿折线段BC-CO以每秒1个单位长的速度向终点O运动、设运动时间为t秒.
(1)当点M运动到A点时,N点距原点O的距离是多少?当点M运动到AB上(不含A点)时,连接MN,t为何值时能使四边形BCNM为梯形?
(2)0≤t<2时,过点N作NP⊥x轴于P点,连接AC交NP于Q,连接MQ
①求△AMQ的面积S与时间t的函数关系式(不必写出t的取值范围)
②当t取何值时,△AMQ的面积最大?最大值为多少?
③当△AMQ的面积达到最大时,其是否为等腰三角形?请说明理由.
解:(1)四边形OABC是等腰梯形,则C(1,2),点M运动到A点时,N运动到C点,ON=OC= ;
;
若四边形BCNM为梯形,则NC=BM,t-2= -2(t-2),解得:t=
-2(t-2),解得:t= .
.
(2)①由于点M以每秒2个单位长的速度向终点B运动,点N以每秒1个单位长的速度向终点O运动,
则点Q横坐标为3-t,纵坐标由 求得:纵坐标为
求得:纵坐标为 (t+1),
(t+1),
s= ×MA×PQ=
×MA×PQ= ×(4-2t)×
×(4-2t)× (t+1)=-
(t+1)=- t2+
t2+ t+
t+ .
.
②当t= 时,最大值是
时,最大值是 .
.
③是,t= ,PM=3-t-2t=
,PM=3-t-2t= ,PA=4-(3-t)=
,PA=4-(3-t)= ,
,
则PM=PA,故△AMQ为等腰三角形.
分析:(1)经分析,点M运动到A点时,N运动到C点,求得OC的长即可.若四边形BCNM为梯形在,则NC=BM,列出关于t的方程求解即可.
(2)△AMQ的面积S= ×MA×PQ,应先求出Q点坐标,Q点横坐标为3-t,纵坐标可由
×MA×PQ,应先求出Q点坐标,Q点横坐标为3-t,纵坐标可由 求得,根据列出的函数关系式,求得最大值.
求得,根据列出的函数关系式,求得最大值.
点评:本题考查了通过动点运动列出函数关系式,并求得最值,综合性强.
 ;
;若四边形BCNM为梯形,则NC=BM,t-2=
 -2(t-2),解得:t=
-2(t-2),解得:t= .
.(2)①由于点M以每秒2个单位长的速度向终点B运动,点N以每秒1个单位长的速度向终点O运动,
则点Q横坐标为3-t,纵坐标由
 求得:纵坐标为
求得:纵坐标为 (t+1),
(t+1),s=
 ×MA×PQ=
×MA×PQ= ×(4-2t)×
×(4-2t)× (t+1)=-
(t+1)=- t2+
t2+ t+
t+ .
.②当t=
 时,最大值是
时,最大值是 .
.③是,t=
 ,PM=3-t-2t=
,PM=3-t-2t= ,PA=4-(3-t)=
,PA=4-(3-t)= ,
,则PM=PA,故△AMQ为等腰三角形.
分析:(1)经分析,点M运动到A点时,N运动到C点,求得OC的长即可.若四边形BCNM为梯形在,则NC=BM,列出关于t的方程求解即可.
(2)△AMQ的面积S=
 ×MA×PQ,应先求出Q点坐标,Q点横坐标为3-t,纵坐标可由
×MA×PQ,应先求出Q点坐标,Q点横坐标为3-t,纵坐标可由 求得,根据列出的函数关系式,求得最大值.
求得,根据列出的函数关系式,求得最大值.点评:本题考查了通过动点运动列出函数关系式,并求得最值,综合性强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
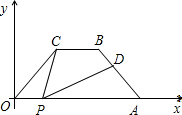 A=45°,点P为x轴上一个动点,(点P不与O、A重合),连接CP,过点P作PD交AB于点D.
A=45°,点P为x轴上一个动点,(点P不与O、A重合),连接CP,过点P作PD交AB于点D. ∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连PD.
∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连PD.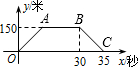 (2012•新昌县模拟)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,其中四边形OABC是等腰梯形,则下列结论中正确的是( )
(2012•新昌县模拟)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,其中四边形OABC是等腰梯形,则下列结论中正确的是( )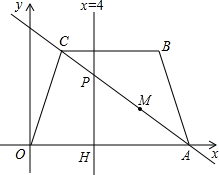 四边形OABC是等腰梯形,OA∥BC,在建立如图的平面直角坐标系中,A(10,0),B(8,6),直线x=4与直线AC交于P点,与x轴交于H点;
四边形OABC是等腰梯形,OA∥BC,在建立如图的平面直角坐标系中,A(10,0),B(8,6),直线x=4与直线AC交于P点,与x轴交于H点; ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.