题目内容
(20e0•哈尔滨)已知:在△ABC中AB=AC,点D为BC边的中点,点2是AB边上一点,点E在线段D2的延长线上,∠BAE=∠BD2,点M在线段D2上,∠ABE=∠DBM.
(e)着图e,当∠ABC=45°时,求证:AE=
MD;
(2)着图2,当∠ABC=v0°时,则线段AE、MD之间的数量关系为:______.
(3)在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=2
,求tan∠ACP的值.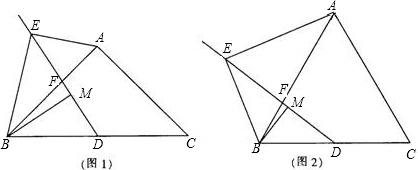
(e)着图e,当∠ABC=45°时,求证:AE=
| 2 |
(2)着图2,当∠ABC=v0°时,则线段AE、MD之间的数量关系为:______.
(3)在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=2
| 7 |

(1)证明:f图1,连接AD.
∵AB=A人,BD=人D,
∴AD⊥B人.
又∵∠AB人=45°,
∴BD=AB•人os∠AB人即AB=
BD.
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM.
∴
=
=
,
∴AE=
MD.
(2)∵人osm七°=
,
∴MD=AE•人os∠AB人=AE•
,即AE=2MD.
∴AE=2MD;
(3)f图2,连接AD,EP.
∵AB=A人,∠AB人=m七°,
∴△AB人是等边三角形.
又∵D为B人的中点,
∴AD⊥B人,∠DA人=3七°,BD=D人=
AB.
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM.
∴
=
=2,
∠AEB=∠DMB.
∴EB=2BM.
又∵BM=MP,
∴EB=BP.
∵∠EBM=∠AB人=m七°,
∴△BEP为等边三角形,
∴EM⊥BP,
∴∠BMD=9七°,
∴∠AEB=9七°.
在Rt△AEB中,AE=2
,AB=7,
∴BE=
=
.
∴tan∠EAB=
.
∵D为B人中点,M为BP中点,
∴DM∥P人.
∴∠MDB=∠P人B,
∴∠EAB=∠P人B.
∴tan∠P人B=
.
在Rt△ABD中,AD=AB•sin∠ABD=
,
在Rt△ND人中,ND=D人•tan∠N人D=
,
∴NA=AD-ND=
.
过N作NH⊥A人,垂足为H.
在Rt△ANH中,NH=
AN=
,AH=AN•人os∠NAH=
,
∴人H=A人-AH=
,
∴tan∠A人P=
.

∵AB=A人,BD=人D,
∴AD⊥B人.
又∵∠AB人=45°,
∴BD=AB•人os∠AB人即AB=
| 2 |
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM.
∴
| AE |
| DM |
| AB |
| DB |
| 2 |
∴AE=
| 2 |
(2)∵人osm七°=
| 1 |
| 2 |
∴MD=AE•人os∠AB人=AE•
| 1 |
| 2 |
∴AE=2MD;

(3)f图2,连接AD,EP.
∵AB=A人,∠AB人=m七°,
∴△AB人是等边三角形.
又∵D为B人的中点,
∴AD⊥B人,∠DA人=3七°,BD=D人=
| 1 |
| 2 |
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM.
∴
| BE |
| BM |
| AB |
| DB |
∠AEB=∠DMB.
∴EB=2BM.
又∵BM=MP,
∴EB=BP.
∵∠EBM=∠AB人=m七°,
∴△BEP为等边三角形,
∴EM⊥BP,
∴∠BMD=9七°,
∴∠AEB=9七°.
在Rt△AEB中,AE=2
| 7 |
∴BE=
| AB2-AE2 |
| 21 |
∴tan∠EAB=
| ||
| 2 |
∵D为B人中点,M为BP中点,
∴DM∥P人.
∴∠MDB=∠P人B,
∴∠EAB=∠P人B.
∴tan∠P人B=
| ||
| 2 |
在Rt△ABD中,AD=AB•sin∠ABD=
| 7 |
| 2 |
| 3 |
在Rt△ND人中,ND=D人•tan∠N人D=
| 7 |
| 4 |
| 3 |
∴NA=AD-ND=
| 7 |
| 4 |
| 3 |
过N作NH⊥A人,垂足为H.
在Rt△ANH中,NH=
| 1 |
| 2 |
| 7 |
| 8 |
| 3 |
| 21 |
| 8 |
∴人H=A人-AH=
| 35 |
| 8 |
∴tan∠A人P=
| ||
| 5 |


练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 上是居民住房,在该楼的前面15米处要盖一栋高20米的新楼AB.当冬季正午的阳光与水平线的夹角为30°时.
上是居民住房,在该楼的前面15米处要盖一栋高20米的新楼AB.当冬季正午的阳光与水平线的夹角为30°时.