题目内容
 如图,不等长的两条对角线AC、BD相交于点O,且将四边形ABCD分成甲、乙、丙、丁四个三角形.若
如图,不等长的两条对角线AC、BD相交于点O,且将四边形ABCD分成甲、乙、丙、丁四个三角形.若 =
= =
= ,则甲、乙、丙、丁这4个三角形中,一定相似的有________.
,则甲、乙、丙、丁这4个三角形中,一定相似的有________.
△AOB∽△COD
分析:由 =
= =
= ,可得AB∥CD;利用两角对应相等,两三角形相似,可证得:甲∽丙,问题可求.
,可得AB∥CD;利用两角对应相等,两三角形相似,可证得:甲∽丙,问题可求.
解答:∵ =
= =
= ,
,
∴AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠CDO,
∴△AOB∽△COD.
故必有甲和丙相似.
点评:本题解答的关键是熟练记住所学的平行线分线段成比例定理,三角形相似的判定方法等.
分析:由
 =
= =
= ,可得AB∥CD;利用两角对应相等,两三角形相似,可证得:甲∽丙,问题可求.
,可得AB∥CD;利用两角对应相等,两三角形相似,可证得:甲∽丙,问题可求.解答:∵
 =
= =
= ,
,∴AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠CDO,
∴△AOB∽△COD.
故必有甲和丙相似.
点评:本题解答的关键是熟练记住所学的平行线分线段成比例定理,三角形相似的判定方法等.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
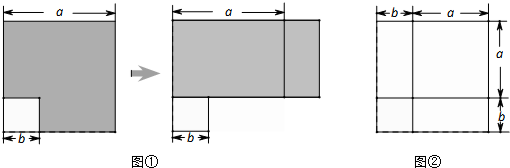
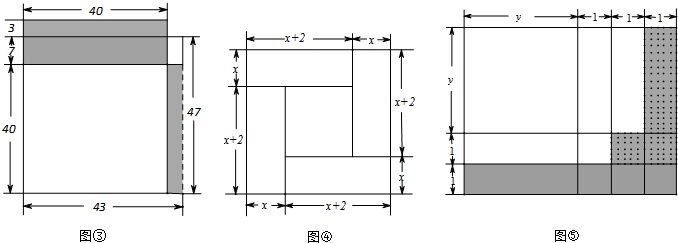

 不妨设
不妨设 ,三条边上的对应高分别为
,三条边上的对应高分别为 ,内接正方形的边长分别为
,内接正方形的边长分别为 .若你对本小题证明有困难,可直接用“
.若你对本小题证明有困难,可直接用“ ”这个结论,但在证明正确的情况下扣1分).
”这个结论,但在证明正确的情况下扣1分).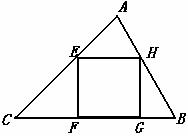




 ,宽为
,宽为 的矩形,构造图④
的矩形,构造图④
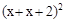 或四个长
或四个长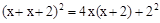




 的解
的解 与
与 的大小关系(其中
的大小关系(其中 )?
)? ,宽
,宽 的矩形,按图⑤方式分割
的矩形,按图⑤方式分割

 ,
, ,即
,即 ,
,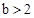 时,表示
时,表示 与
与 的大小关系
的大小关系 ,
,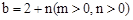 ,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长)
,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长) 不妨设
不妨设 ,三条边上的对应高分别为
,三条边上的对应高分别为 ,内接正方形的边长分别为
,内接正方形的边长分别为 .若你对本小题证明有困难,可直接用“
.若你对本小题证明有困难,可直接用“ ”这个结论,但在证明正确的情况下扣1分).
”这个结论,但在证明正确的情况下扣1分).