题目内容
下面有四种说法:(1)1+2-3+4-5+6-7+8-9+10- ……-2001+2002的结果是偶数;(2)(奇数×奇数)×(奇数—奇数)=奇数;(3)2002个连续自然数的和必是偶数;(4)存在整数a、b,使(a+b)(a-b)=2002.其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
A (1)1+2-3+4-5+6-7+8-9+10- ……-2001+2002=2003-1000=1003是奇数;
(2)(奇数×奇数)×(奇数—奇数)=偶数;
(3)2002个连续自然数的和如:
1+2+3+4+5+ ……+2001+2002中有1001个奇数和1001个偶数,其和分别为奇数和偶数,所以总和应是奇数;
(4)2002=2×7×11×13所以(a+b)和 (a-b)只能一个是奇数一个是偶数,
所以利用加减消元时2a等于一个奇数,
所以a不是整数);

练习册系列答案
相关题目
下面有四种说法,其中正确的是( )
| A、-64的立方根是4 | ||||
| B、49的算术平方根是±7 | ||||
C、
| ||||
D、
|
 的立方根是
的立方根是
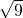 的平方根是±3
的平方根是±3 的立方根是
的立方根是
 的平方根是±3
的平方根是±3