题目内容
 (2010•吴江市模拟)如图,矩形A′B′C′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).O′C′与AB交于D点.
(2010•吴江市模拟)如图,矩形A′B′C′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).O′C′与AB交于D点.(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O,O′两点且图象顶点M的纵坐标为-1,求这个二次函数的解析式;
(2)求D点的坐标;
(3)若将直线OC绕点O旋转α度(0<α<90)后与抛物线的另一个交点为点P,则以O、O′、B、P为顶点的四边形能否是平行四边形?若能,求出tanα的值;若不能,请说明理由.
【答案】分析:(1)因为B点坐标为(1,3),所以C点坐标为(0,3),A点坐标为(1,0),连接OB,O′B,由勾股定理可求出OB的长,根据旋转的性质可知OB=O′B,由勾股定理可求出O′A即可求出O′点的坐标.因为二次函数的图象过O,O′两点,根据二次函数图象上点的坐标特点可求出对称轴直线,可求出M点的坐标.再用待定系数法即可求出函数的解析式.
(2)由于Rt△BC′D≌Rt△O′AD,可知DO′=BD,设AD=x,则可表示出D利用勾股定理;
(3)假设以O、O′、B、P为顶点的四边形是平行四边形,作出图形,求出P点坐标,再通过判断BP1∥=OO',BP2∥=OO',得出四边形是平行四边形的结论.
解答: 解:(1)因为B点坐标为(1,3),
解:(1)因为B点坐标为(1,3),
所以C点坐标为(0,3),A点坐标为(1,0),连接OB,O′B,
所以OA=1,AB=3;根据旋转的性质可知OB=O′B,
根据勾股定理,AO′=
= =
= =
= =1,
=1,
则OO'=1+1=2,O'坐标为(2,0),对称轴为x= =1,
=1,
又因为图象顶点M的纵坐标为-1,
∴M点坐标为(1,-1).
设解析式为y=a(x-1)2-1,
把(0,0)代入解析式
得0=a-1.a=1,原式可化为y=x2-2x.
(2)因为∠C′=∠DAO',∠C'DB=∠ADO',BC=AO',
所以△C'DB≌△ADO',于是BD=O'D.
设AD=x,所以O'D=BD=3-x,在Rt△DAO'中,x2+1=(3-x)2,
解得x= ,
,
所以D点的坐标为(1, ).
).
(3)如图所示,延长CB、BC分别交抛物线于P1,P2.由于B点纵坐标为3且BC平行于x轴,
故P1、P2纵坐标为3,代入抛物线解析式,
得:x2-2x=3,
解得x1=3,x2=-1.
于是BP1=3-1=2,BP2=1-(-1)=2,
故BP1∥OO'且BP1=OO',BP2∥OO'且BP2=OO',
于是OO'P1B和OO'P2B均为平行四边形.
则以O、O′、B、P为顶点的四边形是平行四边形,
tanα= =
= =1或tanα=
=1或tanα= =
= .
.
于是tanα=1或 .
.
点评:考查学生的对存在问题和动点问题的思考方法及数学思想的考查.要注意结合图形,分情况讨论.
(2)由于Rt△BC′D≌Rt△O′AD,可知DO′=BD,设AD=x,则可表示出D利用勾股定理;
(3)假设以O、O′、B、P为顶点的四边形是平行四边形,作出图形,求出P点坐标,再通过判断BP1∥=OO',BP2∥=OO',得出四边形是平行四边形的结论.
解答:
 解:(1)因为B点坐标为(1,3),
解:(1)因为B点坐标为(1,3),所以C点坐标为(0,3),A点坐标为(1,0),连接OB,O′B,
所以OA=1,AB=3;根据旋转的性质可知OB=O′B,
根据勾股定理,AO′=

=
 =
= =
= =1,
=1,则OO'=1+1=2,O'坐标为(2,0),对称轴为x=
 =1,
=1,又因为图象顶点M的纵坐标为-1,
∴M点坐标为(1,-1).
设解析式为y=a(x-1)2-1,
把(0,0)代入解析式
得0=a-1.a=1,原式可化为y=x2-2x.
(2)因为∠C′=∠DAO',∠C'DB=∠ADO',BC=AO',
所以△C'DB≌△ADO',于是BD=O'D.
设AD=x,所以O'D=BD=3-x,在Rt△DAO'中,x2+1=(3-x)2,
解得x=
 ,
,所以D点的坐标为(1,
 ).
).(3)如图所示,延长CB、BC分别交抛物线于P1,P2.由于B点纵坐标为3且BC平行于x轴,
故P1、P2纵坐标为3,代入抛物线解析式,

得:x2-2x=3,
解得x1=3,x2=-1.
于是BP1=3-1=2,BP2=1-(-1)=2,
故BP1∥OO'且BP1=OO',BP2∥OO'且BP2=OO',
于是OO'P1B和OO'P2B均为平行四边形.
则以O、O′、B、P为顶点的四边形是平行四边形,
tanα=
 =
= =1或tanα=
=1或tanα= =
= .
.于是tanα=1或
 .
.点评:考查学生的对存在问题和动点问题的思考方法及数学思想的考查.要注意结合图形,分情况讨论.

练习册系列答案
相关题目
 (2010•吴江市模拟)如图,矩形A′B′C′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).O′C′与AB交于D点.
(2010•吴江市模拟)如图,矩形A′B′C′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).O′C′与AB交于D点.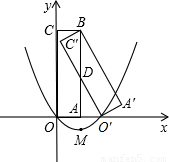 (2010•吴江市模拟)如图,矩形A′B′C′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).O′C′与AB交于D点.
(2010•吴江市模拟)如图,矩形A′B′C′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).O′C′与AB交于D点.