题目内容
 如图,一圆桌周围有20个箱子,依顺时针方向编号1~20.小明在1号箱子中丢入一颗红球后,沿着圆桌依顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球:
如图,一圆桌周围有20个箱子,依顺时针方向编号1~20.小明在1号箱子中丢入一颗红球后,沿着圆桌依顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球:
(1)若前一个箱子丢红球,经过的箱子就丢绿球;
(2)若前一个箱子丢绿球,经过的箱子就丢白球;
(3)若前一个箱子丢白球,经过的箱子就丢红球.
若他沿着圆桌走了50圈后,则2号箱内有______颗绿球.
解:第1圈绿球在2、5、8、11、14、17、20号箱内,
第2圈绿球在3、6、9、12、15、18号箱内,
第3圈绿球在1、4、7、10、13、16、19号箱内,
第4圈绿球在在2、5、8、11、14、17、20号箱内,
…
且在2、5、8、11、14、17、20号箱内,丢一颗绿球,
an=a1+(n-1)d,
50=2+3(n-1),
16=n-1,
n=17,
故答案为:17
分析:根据已知要求得出第2、5、8、11、14、17、20圈会在2号箱内丢一颗绿球,进而得出通项公式an=a1+(n-1)d,得出答案即可.
点评:此题主要考查了图形的变化类,根据已知规律得出通项公式是解题关键.
第2圈绿球在3、6、9、12、15、18号箱内,
第3圈绿球在1、4、7、10、13、16、19号箱内,
第4圈绿球在在2、5、8、11、14、17、20号箱内,
…
且在2、5、8、11、14、17、20号箱内,丢一颗绿球,
an=a1+(n-1)d,
50=2+3(n-1),
16=n-1,
n=17,
故答案为:17
分析:根据已知要求得出第2、5、8、11、14、17、20圈会在2号箱内丢一颗绿球,进而得出通项公式an=a1+(n-1)d,得出答案即可.
点评:此题主要考查了图形的变化类,根据已知规律得出通项公式是解题关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
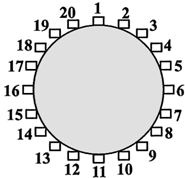 (2012•台湾)如图,一圆桌周围有20个箱子,依顺时针方向编号1~20.小明在1号箱子中丢入一颗红球后,沿着圆桌依顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球:
(2012•台湾)如图,一圆桌周围有20个箱子,依顺时针方向编号1~20.小明在1号箱子中丢入一颗红球后,沿着圆桌依顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球: (2013•锡山区一模)如图,一圆桌周围有20个箱子,依顺时针方向编号1~20.小明在1号箱子中丢入一颗红球后,沿着圆桌依顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球:
(2013•锡山区一模)如图,一圆桌周围有20个箱子,依顺时针方向编号1~20.小明在1号箱子中丢入一颗红球后,沿着圆桌依顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球:
