题目内容
如图，从山顶A望地面C、D两点，测得他们的俯角分别是45°和30°，已知CD=100米，点C位于BD上，求山AB的高度．（结果可保留根号）
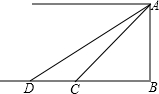
如图，设AB=xm，
∵∠MAC=45°，∠MAD=30°，
∴∠D=30°，∠ACB=45°，
在Rt△ABC中，BC=AB=x，
在Rt△ADB中，DB=CD+BC=100+x，
∴DB=
AB，即100+x=
x，解得x=50（
+1）m．
所以山AB的高度为50（
+1）米．
∵∠MAC=45°，∠MAD=30°，
∴∠D=30°，∠ACB=45°，
在Rt△ABC中，BC=AB=x，
在Rt△ADB中，DB=CD+BC=100+x，
∴DB=
| 3 |
| 3 |
| 3 |
所以山AB的高度为50（
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
是43度．1s后，火箭到达B点，此时测得BC的距离是6.13km，仰角为45.54°，解答下列问题：
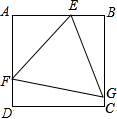
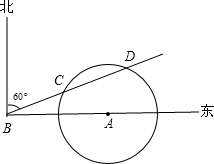北偏东60°的BD方向移动，在距离台风中心130km内的地方都要受到其影响．