题目内容
【题目】如图,已知直线l1∥l2,且l3与l1,l2分别交于A,B两点,l4与l1,l2相交于C,D两点,点P在直线AB上.
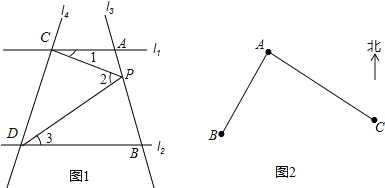
(1)【探究1】如图1,当点P在A,B两点间滑动时,试探究∠1,∠2,∠3之间的关系是否发生变化?并说明理由;
(2)【应用】如图2,A点在B处北偏东32°方向,A点在C处的北偏西56°方向,应用探究1的结论求出∠BAC的度数.
(3)【探究2】如果点P在A,B两点外侧运动时,试探究∠ACP,∠BDP,∠CPD之间的关系,并说明理由.
【答案】见解析
【解析】
试题分析:(1)过点P作PQ∥AC,交CD于点Q,由PQ∥l1∥l2结合“两直线平行,内错角相等”找出“∠1=∠CPQ,∠3=∠DPQ”,再通过角的计算即可得出结论;
(2)分别在B点和A点处画方位图,结合(1)的结论即可算出结果;
(3)分点P的位置不同来考虑:①当点P在A点上方时,过点P作PQ∥AC,交CD于点Q,由PQ∥l1∥l2结合“两直线平行,内错角相等”找出“∠QPC=∠ACP,∠QPD=∠BDP”,再通过角的计算即可得出结论;②当点P在B点下方时,过点P作PQ∥AC,交CD于点Q,利用①的方法可得出结论.综合①②即可得出结论.
解:(1)当点P在A、B两点间滑动时,∠2=∠1+∠3保持不变.理由如下:
过点P作PQ∥AC,交CD于点Q,如图1所示.

∵PQ∥AC,
∴∠1=∠CPQ,
又∵PQ∥AC,BD∥AC,
∴PQ∥BD,
∴∠3=∠DPQ,
∴∠1+∠3=∠CPQ+∠DPQ,
即∠1+∠3=∠2.
(2)分别在B点和A点处画方位图,如图2所示.

由(1)知:∠2=∠1+∠3
∴∠BAC=32°+56°=88°.
(3)①当点P在A点上方时,过点P作PQ∥AC,交CD于点Q,如图3所示.

∵PQ∥AC,
∴∠QPC=∠ACP.
又∵PQ∥AC,BD∥AC,
∴PQ∥BD,
∴∠QPD=∠BDP.
又∵∠CPD=∠QPD﹣∠QPC,
∴∠CPD=∠BDP﹣∠ACP.
②当点P在B点下方时,过点P作PQ∥AC,交CD于点Q,如图3所示.

同理可得:∠CPD=∠ACP﹣∠BDP.
综上:∠CPD=|∠ACP﹣∠BDP|.