题目内容
矩形OABC在平面直角坐标系中位置如图所示,A、C两点的坐标分别为A(6,0),C(0,-3),直线y=- x与BC边相交于D点.
x与BC边相交于D点.(1)求点D的坐标;
(2)若抛物线y=ax2-
 x经过点A,试确定此抛物线的表达式;
x经过点A,试确定此抛物线的表达式;(3)设(2)中的抛物线的对称轴与直线OD交于点M,点P为对称轴上一动点,以P、O、M为顶点的三角形与△OCD相似,求符合条件的点P的坐标.

【答案】分析:前两问由抛物线性质,用待定系数求出点D的坐标和抛物线的表达式;最后一问找三角形相似,作辅助线过点O作OD的垂线交抛物线的对称轴于点P2,再根据相似三角形比例关系求出P点坐标.
解答:解:(1)∵直线y=- x与BC边相交于D点,知D点纵坐标为-3,
x与BC边相交于D点,知D点纵坐标为-3,
∴代入直线得点D的坐标为(4,-3).(2分)
(2)∵A(6,0)在抛物线上,代入抛物线的表达式得a= ,
,
∴y= x2-
x2- x.(4分)
x.(4分)
(3)抛物线的对称轴与x轴的交点P1符合条件.
∵OA∥CB,
∴∠P1OM=∠CDO.
∵∠OP1M=∠DCO=90°,
∴Rt△P1OM∽Rt△CDO.(6分)
∵抛物线的对称轴x=3,
∴点P1的坐标为P1(3,0).(7分)
过点O作OD的垂线交抛物线的对称轴于点P2.
∵对称轴平行于y轴,
∴∠P2MO=∠DOC.
∵∠P2OM=∠DCO=90°,
∴Rt△P2MO∽Rt△DOC.(8分)
∴点P2也符合条件,∠OP2M=∠ODC.
∴P1O=CO=3,∠P2P1O=∠DCO=90°,
∴Rt△P2P1O≌Rt△DCO.(9分)
∴P1P2=CD=4.
∵点P2在第一象限,
∴点P2的坐标为P2(3,4),
∴符合条件的点P有两个,分别是P1(3,0),P2(3,4).(11分)
点评:此题考查函数性质与坐标关系,最后一问探究点的存在性问题,几何图形形式问题和直角三角形性质.
解答:解:(1)∵直线y=-
 x与BC边相交于D点,知D点纵坐标为-3,
x与BC边相交于D点,知D点纵坐标为-3,∴代入直线得点D的坐标为(4,-3).(2分)
(2)∵A(6,0)在抛物线上,代入抛物线的表达式得a=
 ,
,∴y=
 x2-
x2- x.(4分)
x.(4分)(3)抛物线的对称轴与x轴的交点P1符合条件.

∵OA∥CB,
∴∠P1OM=∠CDO.
∵∠OP1M=∠DCO=90°,
∴Rt△P1OM∽Rt△CDO.(6分)
∵抛物线的对称轴x=3,
∴点P1的坐标为P1(3,0).(7分)
过点O作OD的垂线交抛物线的对称轴于点P2.
∵对称轴平行于y轴,
∴∠P2MO=∠DOC.
∵∠P2OM=∠DCO=90°,
∴Rt△P2MO∽Rt△DOC.(8分)
∴点P2也符合条件,∠OP2M=∠ODC.
∴P1O=CO=3,∠P2P1O=∠DCO=90°,
∴Rt△P2P1O≌Rt△DCO.(9分)
∴P1P2=CD=4.
∵点P2在第一象限,
∴点P2的坐标为P2(3,4),
∴符合条件的点P有两个,分别是P1(3,0),P2(3,4).(11分)
点评:此题考查函数性质与坐标关系,最后一问探究点的存在性问题,几何图形形式问题和直角三角形性质.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
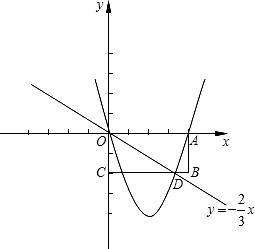 的坐标(0,-2),直线y=-
的坐标(0,-2),直线y=-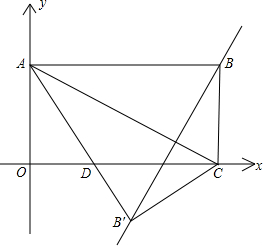 如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足
如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足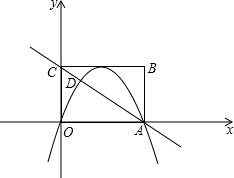 (2013•昆明)如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.
(2013•昆明)如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D. (2012•合山市模拟)矩形OABC在平面直角坐标系中的位置如图所示,其中OA=5,AB=2,抛物线y=-x2+3x的图象与BC交于D、E两点.
(2012•合山市模拟)矩形OABC在平面直角坐标系中的位置如图所示,其中OA=5,AB=2,抛物线y=-x2+3x的图象与BC交于D、E两点.