题目内容
 如图,以线段AB为直径的⊙O交线段AC于点E,点M是
如图,以线段AB为直径的⊙O交线段AC于点E,点M是 的中点,OM交AC于点D,∠BOE=60°,cosC=
的中点,OM交AC于点D,∠BOE=60°,cosC= ,BC=2
,BC=2 .
.
(1)求∠A的度数;
(2)求证:BC是⊙O的切线;
(3)求MD的长度.
(1)解:∵∠BOE=60°,
∴∠A= ∠BOE=30°.
∠BOE=30°.
(2)证明:在△ABC中,∵cosC= ,
,
∴∠C=60°.
又∵∠A=30°,
∴∠ABC=90°,
∴AB⊥BC.
∴BC是⊙O的切线.
(3)解:∵点M是 的中点,
的中点,
∴OM⊥AE.
在Rt△ABC中,∵BC=2 ,
,
∴AB=BC•tan60°=2 ×
× =6.
=6.
∴OA= =3,
=3,
∴OD= OA=
OA= ,
,
∴MD= .
.
分析:(1)根据三角函数的知识即可得出∠A的度数.
(2)要证BC是⊙O的切线,只要证明AB⊥BC即可.
(3)根据切线的性质,运用三角函数的知识求出MD的长度.
点评:本题综合考查了三角函数的知识、切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
∴∠A=
 ∠BOE=30°.
∠BOE=30°.(2)证明:在△ABC中,∵cosC=
 ,
,∴∠C=60°.
又∵∠A=30°,
∴∠ABC=90°,
∴AB⊥BC.
∴BC是⊙O的切线.
(3)解:∵点M是
 的中点,
的中点,∴OM⊥AE.
在Rt△ABC中,∵BC=2
 ,
,∴AB=BC•tan60°=2
 ×
× =6.
=6.∴OA=
 =3,
=3,∴OD=
 OA=
OA= ,
,∴MD=
 .
.分析:(1)根据三角函数的知识即可得出∠A的度数.
(2)要证BC是⊙O的切线,只要证明AB⊥BC即可.
(3)根据切线的性质,运用三角函数的知识求出MD的长度.
点评:本题综合考查了三角函数的知识、切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
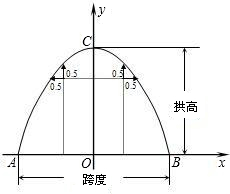 的表达式、隧道的跨度AB和拱高OC.
的表达式、隧道的跨度AB和拱高OC.