题目内容
过点P（2，3）作直线，使它与两坐标轴围成的三角形面积为12，这样的直线可以作________条．
4
分析：设直线的解析式是y=kx+b，直线经过点（2，3）则得到：2k+b=3．再根据三角形的面积是12，就可得到一个关于k，b的方程组．判断方程组解得个数即可．
解答：y=kx+b，直线经过点（2，3）则得到：2k+b=3…（1）
在y=kx+b中，令x=0，解得y=b．
令y=0，x=-
．根据直线与两坐标轴围成的三角形面积为12．
得到：
|-|•|b|=12．即b2=24|k|…（2）
由（1）得：b=3-2k．代入（2）得：9-12k+4k2=24|k|…（3）
当k＞0时，（3）变形为：4k2-36k+9=0．这个方程有两个不同的正根．即k有两个正值；
当k＜0时，（3）变形为：4k2+12k+9=0．方程有两个相同的负根，即k有一个负值；
总之，k的值有3个．
点评：把判断直线的条数的问题转化为判断一元二次方程的解的个数的问题是解决本题的关键．
分析：设直线的解析式是y=kx+b，直线经过点（2，3）则得到：2k+b=3．再根据三角形的面积是12，就可得到一个关于k，b的方程组．判断方程组解得个数即可．
解答：y=kx+b，直线经过点（2，3）则得到：2k+b=3…（1）
在y=kx+b中，令x=0，解得y=b．
令y=0，x=-
．根据直线与两坐标轴围成的三角形面积为12．得到：
|-|•|b|=12．即b2=24|k|…（2）由（1）得：b=3-2k．代入（2）得：9-12k+4k2=24|k|…（3）
当k＞0时，（3）变形为：4k2-36k+9=0．这个方程有两个不同的正根．即k有两个正值；
当k＜0时，（3）变形为：4k2+12k+9=0．方程有两个相同的负根，即k有一个负值；
总之，k的值有3个．
点评：把判断直线的条数的问题转化为判断一元二次方程的解的个数的问题是解决本题的关键．
练习册系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
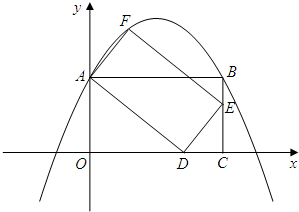、n的代数式表示该抛物线；若不存在，请说明理由．
如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-2，4），过点A作AB⊥y轴，垂足为B，连接OA．