题目内容
 已知,如图,一工厂车间门口由抛物线和矩形ABCO的三边组成,门的最大高度是4.9米,AB=10米,BC=2.4米,若有一个高为4米,宽为2米的长方体形的大型设备要安装在车间,如果不考虑其他因素,设备的右侧离开门边多少米,此设备运进车间时才不致于碰门的顶部
已知,如图,一工厂车间门口由抛物线和矩形ABCO的三边组成,门的最大高度是4.9米,AB=10米,BC=2.4米,若有一个高为4米,宽为2米的长方体形的大型设备要安装在车间,如果不考虑其他因素,设备的右侧离开门边多少米,此设备运进车间时才不致于碰门的顶部
- A.1.8
- B.1.9
- C.2.0
- D.2.1
C
分析:以AB为x轴,AB的中点为坐标原点建立平面直角坐标系,表示出抛物线上三个点的坐标,求得抛物线的解析式,再代入对应数值解答即可.
解答:如图,以AB为x轴,AB的中点为坐标原点建立平面直角坐标系.

则A点坐标为(-5,0),O点坐标为(-5,2.4),C点坐标为(5,2.4),D点坐标为(0,4.9),
设抛物线解析式为:y=ax2+4.9,
把O点坐标代入,解得a=- ,
,
所以y=- x2+4.9,
x2+4.9,
把y=4代入y=- x2+4.9,
x2+4.9,
解得x=±3;
即设备的右侧离开门边5-3=2米时,此设备运进车间时才不致于碰门的顶部.
故选C.
点评:解答此题关键是建立适当的坐标系,求得解析式,再根据题中数据要求代入计算即可.
分析:以AB为x轴,AB的中点为坐标原点建立平面直角坐标系,表示出抛物线上三个点的坐标,求得抛物线的解析式,再代入对应数值解答即可.
解答:如图,以AB为x轴,AB的中点为坐标原点建立平面直角坐标系.

则A点坐标为(-5,0),O点坐标为(-5,2.4),C点坐标为(5,2.4),D点坐标为(0,4.9),
设抛物线解析式为:y=ax2+4.9,
把O点坐标代入,解得a=-
 ,
,所以y=-
 x2+4.9,
x2+4.9,把y=4代入y=-
 x2+4.9,
x2+4.9,解得x=±3;
即设备的右侧离开门边5-3=2米时,此设备运进车间时才不致于碰门的顶部.
故选C.
点评:解答此题关键是建立适当的坐标系,求得解析式,再根据题中数据要求代入计算即可.

练习册系列答案
相关题目
 24、已知,如图为一日历的一部分,粗线所在的框刚好框住了9个数,设中间的一个数为x,那么这9个数的和为
24、已知,如图为一日历的一部分,粗线所在的框刚好框住了9个数,设中间的一个数为x,那么这9个数的和为 B重合),且保持DE∥AB.以DE为边向上作正方形DEFG.
B重合),且保持DE∥AB.以DE为边向上作正方形DEFG.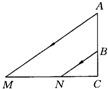 已知:如图是一束光线射入室内的平面图,上檐边缘射入的光线照在距窗户2.5m处,已知窗户AB高为2m,B点距地面高为1.2m,求下檐光线的落地点N与窗户的距离NC.
已知:如图是一束光线射入室内的平面图,上檐边缘射入的光线照在距窗户2.5m处,已知窗户AB高为2m,B点距地面高为1.2m,求下檐光线的落地点N与窗户的距离NC.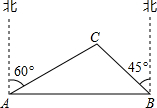 已知:如图,一艘渔船正在港口A的正东方向40海里的B处进行捕鱼作业,突然接到通知,要该船前往C岛运送一批物资到A港,已知C岛在A港的北偏东60°方向,且在B的北偏西45°方向.问该船从B处出发,以平均每小时20海里的速度行驶,需要多少时间才能把这批物资送到A港(精确到1小时)(该船在C岛停留半个小时)?
已知:如图,一艘渔船正在港口A的正东方向40海里的B处进行捕鱼作业,突然接到通知,要该船前往C岛运送一批物资到A港,已知C岛在A港的北偏东60°方向,且在B的北偏西45°方向.问该船从B处出发,以平均每小时20海里的速度行驶,需要多少时间才能把这批物资送到A港(精确到1小时)(该船在C岛停留半个小时)?