题目内容
 如图,直线AB与⊙O相切于点C,弦EF∥AB交OC于H,D是⊙O上一点,连接DE、DC、OF.
如图,直线AB与⊙O相切于点C,弦EF∥AB交OC于H,D是⊙O上一点,连接DE、DC、OF.
(1)若∠EDC=30°,则∠COF=______度;
(2)若EF= ,CH=2,求⊙O的半径.
,CH=2,求⊙O的半径.
解:(1)∵直线AB与⊙O相切于点C,
∴OC⊥AB;
∵EF∥AB,
∴OC⊥EF,
∴ =
=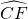 ,
,
∴∠COF=2∠EDC=2×30°=60°.
(2)设⊙O的半径为r;
在Rt△OHF中,
∵∠COF=60°,
∴∠OFH=30°,
∴OH= OF=
OF= ,
,
∵EF= ,
,
∴HF=2 ,
,
由勾股定理得:OF2=OH2+HF2,即r2=( )2+(2
)2+(2 )2,
)2,
解得:r=4.
分析:(1)根据切线的性质可知,OC⊥AB,由于EF∥AB,故OC⊥EF,由垂径定理可知 =
=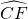 ,根据同圆或等圆中同弧或等弧所对的圆周角等于圆心角的一半解答即可.
,根据同圆或等圆中同弧或等弧所对的圆周角等于圆心角的一半解答即可.
(2)设⊙O的半径为r,根据直角三角形的性质及勾股定理列出方程解答即可.
点评:此题貌似复杂,实属简单题目:
(1)利用平行线的性质及圆周角定理即可解答;
(2)利用的是直角三角形的性质及勾股定理.
∴OC⊥AB;
∵EF∥AB,
∴OC⊥EF,
∴
 =
=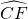 ,
,∴∠COF=2∠EDC=2×30°=60°.
(2)设⊙O的半径为r;
在Rt△OHF中,
∵∠COF=60°,
∴∠OFH=30°,
∴OH=
 OF=
OF= ,
,∵EF=
 ,
,∴HF=2
 ,
,由勾股定理得:OF2=OH2+HF2,即r2=(
 )2+(2
)2+(2 )2,
)2,解得:r=4.
分析:(1)根据切线的性质可知,OC⊥AB,由于EF∥AB,故OC⊥EF,由垂径定理可知
 =
=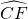 ,根据同圆或等圆中同弧或等弧所对的圆周角等于圆心角的一半解答即可.
,根据同圆或等圆中同弧或等弧所对的圆周角等于圆心角的一半解答即可.(2)设⊙O的半径为r,根据直角三角形的性质及勾股定理列出方程解答即可.
点评:此题貌似复杂,实属简单题目:
(1)利用平行线的性质及圆周角定理即可解答;
(2)利用的是直角三角形的性质及勾股定理.

练习册系列答案
相关题目
 9、如图,直线AB与⊙O相切于点B,BC是⊙O的直径,AC交⊙O于点D,连接BD,则图中直角三角形有
9、如图,直线AB与⊙O相切于点B,BC是⊙O的直径,AC交⊙O于点D,连接BD,则图中直角三角形有 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD,∠AOD=40°.求:∠POB,∠EOF的度数.
如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD,∠AOD=40°.求:∠POB,∠EOF的度数. 如图,直线AB与x轴、y轴分别交于点A、B,点A的坐标是(2,0),∠ABO=30°.在坐标平面内,是否存在点P(除点O外),使得△APB与△AOB全等.请写出所有符合条件的点P的坐标
如图,直线AB与x轴、y轴分别交于点A、B,点A的坐标是(2,0),∠ABO=30°.在坐标平面内,是否存在点P(除点O外),使得△APB与△AOB全等.请写出所有符合条件的点P的坐标 如图,直线AB与CD相交于O点,∠AOE=∠DOF=90°,OP是∠BOC的平分线,其中∠AOD=40°,则∠EOP的度数为 ( )
如图,直线AB与CD相交于O点,∠AOE=∠DOF=90°,OP是∠BOC的平分线,其中∠AOD=40°,则∠EOP的度数为 ( ) 如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,若∠AOC=65°,则∠DOE的度数是
如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,若∠AOC=65°,则∠DOE的度数是