题目内容
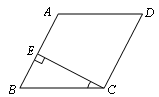
如图,□ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF= ,求AB的长.
,求AB的长.
 ,求AB的长.
,求AB的长.
1.
试题分析:首先证明四边形ABDE是平行四边形,AB=DE=CD,即D是CE的中点,在直角△CEF中利用三角函数即可求得到CE的长,则求得CD,进而根据AB=CD求解.
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形.
∴AB=DE=CD,即D为CE中点.
∵EF⊥BC,
∴∠EFC=90°.
∵AB∥CD,
∴∠DCF=∠ABC=60°.
∴∠CEF=30°.
∵EF=
 ,
,∴CE=2.
∴AB=1.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目



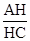 的值为 .
的值为 .