Question

【题目】已知函数的图象与轴有两个公共点．

（1）求的取值范围，写出当取范围内最大整数时函数的解析式；

（2）题（1）中求得的函数记为C1

①当时，的取值范围是，求的值；

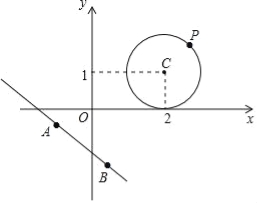
②函数C2：的图象由函数C1的图象平移得到，其顶点P落在以原

点为圆心，半径为的圆内或圆上.设函数C1的图象顶点为M，求点P与点M距

离最大时函数C2的解析式．

Answer 1

【答案】（1）且当时，函数解析式为：；（2）①；②PM最大时的函数解析式为．

【解析】

试题分析： （1）函数的图象与轴有两个公共点．可知，根的判别式△＞0，且m≠0，求得m的范围且在此范围内m取得最大整数2，解析式可写出；（2）①根据函数增减性可以发现当x=n时，y=-3n，代入解析式求出；②求出C1的顶点M坐标为

由图像可知当PM经过圆心O时距离最大，求出直线PM的解析式为设出P点坐标，根据勾股定理就能求得P点坐标（2,1），C2解析式为.

试题解析：（1）由题意可得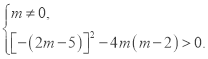：解得：且

当时，函数解析式为：．

（2）①函数图象开口向上，对称轴为

∴当时，随的增大而减小．

∵当时，的取值范围是，

∴ ．

∴ 或（舍去）．

∴ ．

②∵

∴图象顶点的坐标为，

由图形可知当为射线与圆的交点时，距离最大．

∵点P在直线OM上,由可求得直线解析式为：，

设P（a,b），则有a=2b，

根据勾股定理可得

求得．

∴PM最大时的函数解析式为．