题目内容
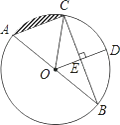
【题目】如图,正方形ABCD的边长是4,点E是BC的中点,连接DE,DF⊥DE交BA的延长线于点F.连接EF、AC,DE、EF分别与C交于点P、Q,则PQ=_____.

【答案】![]()
【解析】
过点E作EM∥AB,交AC于点M,由题意可证ME∥AB∥CD,△ADF≌△CDE,可得AF=CE=ME,根据平行线分线段成比例可得![]() ,
,![]() ,
,![]() ,即可求PQ的长.
,即可求PQ的长.
如图,过点E作EM∥AB,交AC于点M,

∵四边形ABCD是正方形
∴AD=CD=BC=4,∠ADC=∠DAB=∠DCE=90°,∠ACE=45°,AB∥CD,
∴∠CDE+∠ADE=90°,AC=4![]()
∵DF⊥DE,
∴∠FDA+∠ADE=90°
∴∠CDE=∠FDA,且∠DAF=∠DCE=90°,AD=CD,
∴△ADF≌△CDE(AAS)
∴AF=CE,
∵点E是BC中点,
∴CE=BE=![]() BC=AF,
BC=AF,
∵ME∥CD
∴∠DCE=∠MEB=90°,且∠ACB=45°
∴∠CME=∠ACB=45°,
∴ME=CE=![]() BC,
BC,
∵ME∥AB,AB∥CD,
∴ME∥AB∥CD,
∴![]() ,
,![]() ,
,![]() ,
,
∴MQ=AQ,AM=CM=2![]() ,CP=2MP,
,CP=2MP,
∴MQ=![]() ,MP=
,MP=![]()
∴PQ=MQ+MP=![]()

 新思维寒假作业系列答案
新思维寒假作业系列答案【题目】某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为x(0<x<0.5).
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ① |
平均步长(米/步) | 0.6 | ② |
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.