题目内容
如图,四边形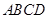 内接于
内接于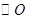 ,
,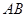 为
为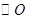 的直径,
的直径,
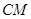 切
切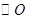 于点
于点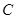 ,
, 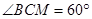 ,则
,则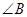 的正切值是( )
的正切值是( )
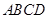 内接于
内接于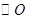 ,
,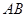 为
为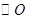 的直径,
的直径,
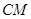 切
切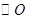 于点
于点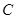 ,
, 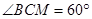 ,则
,则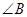 的正切值是( )
的正切值是( )A.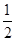 | B.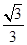 | C.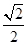 | D.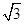 |
B
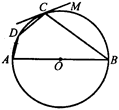
连接BD.AB是直径,则∠ADB=90°,由弦切角定理知∠CDB=∠BCM=60°,∠CDA=150°.
再由圆内接四边形的对角互补可求∠CBA=30°,根据三角函数的求法可知tan∠ABC= .
.

解:连接BD.
AB是直径,则∠ADB=90°,
∴∠CDB=∠BCM=60°.
∴∠CDA=∠CDB+∠ADB=150°.
∵∠CBA=180°-∠CDA=30°,
∴tan∠ABC=tan30°= .
.
故选B.
本题利用了直径对的圆周角是直角,弦切角定理,圆内接四边形的性质求解.
再由圆内接四边形的对角互补可求∠CBA=30°,根据三角函数的求法可知tan∠ABC=
 .
.
解:连接BD.
AB是直径,则∠ADB=90°,
∴∠CDB=∠BCM=60°.
∴∠CDA=∠CDB+∠ADB=150°.
∵∠CBA=180°-∠CDA=30°,
∴tan∠ABC=tan30°=
 .
.故选B.
本题利用了直径对的圆周角是直角,弦切角定理,圆内接四边形的性质求解.

练习册系列答案
相关题目
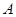 为圆心,3cm为半径作⊙
为圆心,3cm为半径作⊙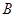 为圆心,2cm为半径作⊙
为圆心,2cm为半径作⊙ 是
是 的直径,
的直径, 是
是

 .
.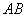 为半圆
为半圆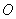 的直径,延长
的直径,延长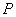 ,使
,使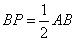 ,
,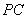 切半圆
切半圆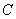 ,点
,点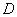 是弧AC上和点
是弧AC上和点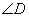 的度数为 .(圆的性质、切线的性质、解三角形)
的度数为 .(圆的性质、切线的性质、解三角形) 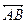 的中点,CD是⊙O的直径,过C点的直线
的中点,CD是⊙O的直径,过C点的直线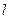 交AB所在直线于点E,交⊙O于点F。
交AB所在直线于点E,交⊙O于点F。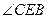 与
与 的数量关系,并写出结论;
的数量关系,并写出结论;


 ,并说明理由;
,并说明理由;