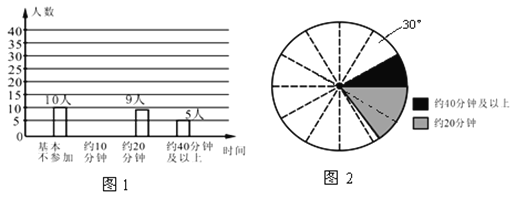
ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮOABCЕФЖЅЕуOдкзјБъдЕуЃЌЧвOAБпКЭABБпЫљдкжБЯпЕФНтЮіЪНЗжБ№ЮЊЃК![]() КЭ
КЭ![]() ЃЎ
ЃЎ
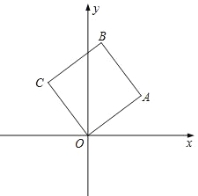
ЃЈ1ЃЉЧѓе§ЗНаЮOABCЕФБпГЄЃЛ
ЃЈ2ЃЉЯжгаЖЏЕуPЁЂQЗжБ№ДгCЁЂAЭЌЪБГіЗЂЃЌЕуPбиЯпЖЮCBЯђжеЕуBдЫЖЏЃЌЫйЖШЮЊУПУы1ИіЕЅЮЛЃЌЕуQбиелЯпAЁњOЁњCЯђжеЕуCдЫЖЏЃЌЫйЖШЮЊУПУыkИіЕЅЮЛЃЌЩшдЫЖЏЪБМфЮЊ2УыЃЎЕБkЮЊКЮжЕЪБЃЌНЋЁїCPQбиЫќЕФвЛБпЗелЃЌЪЙЕУЗелЧАКѓЕФСНИіШ§НЧаЮзщГЩЕФЫФБпаЮЮЊСтаЮЃП
ЃЈ3ЃЉШєе§ЗНаЮвдУПУы![]() ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOЯТЛЌЃЌжБжСЖЅЕуCТфдкxжсЩЯЪБЭЃжЙЯТЛЌЃЎЩше§ЗНаЮдкxжсЯТЗНВПЗжЕФУцЛ§ЮЊSЃЌЧѓSЙигкЛЌааЪБМфtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOЯТЛЌЃЌжБжСЖЅЕуCТфдкxжсЩЯЪБЭЃжЙЯТЛЌЃЎЩше§ЗНаЮдкxжсЯТЗНВПЗжЕФУцЛ§ЮЊSЃЌЧѓSЙигкЛЌааЪБМфtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ5ЃЛЃЈ2ЃЉk=2Лђk=4ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉСЊСЂЗНГЬзщЧѓЕУЕуAЕФзјБъМДПЩЕУЕННсЙћЃЛ
ЃЈ2ЃЉгаСНжжЧщПіЃКЂйQдкOAЩЯЃЌдђCQ=PQЪБФмЙЙГЩСтаЮЃЌИљОнЬтвтСаГі2k=4МДПЩЧѓЕУЃЛЂкQЕудкOCЩЯЃЌдђPC=QCЪБВХФмЙЙГЩСтаЮЃЌИљОнЬтвтСаГі2k=8МДПЩЧѓЕУЃЛ
ЃЈ3ЃЉЂйЕБЕуAдЫЖЏЕНЕуOЪБЃЌt=3ЃЌЕБ0ЃМtЁм3ЪБЃЌЩшOЁфCЁфНЛxжсгкЕуDЃЌИљОнШ§НЧКЏЪ§ЕФЖЈвхtanЁЯDOOЁф=![]() ЃЌМД
ЃЌМД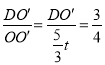 ЃЌЧѓЕУDOЁф=
ЃЌЧѓЕУDOЁф=![]() tМДПЩЕУЕНS=
tМДПЩЕУЕНS=![]() DOЁфOOЁф=
DOЁфOOЁф=![]()
![]() t
t![]() t=
t=![]() t2ЃЛЂкЕБЕуCдЫЖЏЕНxжсЩЯЪБЃЌt=ЃЈ5ЁС
t2ЃЛЂкЕБЕуCдЫЖЏЕНxжсЩЯЪБЃЌt=ЃЈ5ЁС![]() ЃЉЁТ
ЃЉЁТ![]() =4ЃЌЕБ3ЃМtЁм4ЪБЃЌЩшAЁфBЁфНЛxжсгкЕуEгЩгкAЁфO=
=4ЃЌЕБ3ЃМtЁм4ЪБЃЌЩшAЁфBЁфНЛxжсгкЕуEгЩгкAЁфO=![]() t-5ЃЌгкЪЧЕУЕНAЁфE=
t-5ЃЌгкЪЧЕУЕНAЁфE=![]() AЁфO=
AЁфO=![]() МДПЩЕУЕНS=
МДПЩЕУЕНS=![]() ЃЈAЁфE+OЁфDЃЉAЁфOЁф=
ЃЈAЁфE+OЁфDЃЉAЁфOЁф=![]() ЃЈ
ЃЈ![]() +
+![]() tЃЉ5=
tЃЉ5=![]() ЃЎ
ЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉСЊСЂ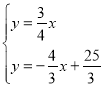 ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрAЃЈ4ЃЌ3ЃЉЃЌ
ЁрOA=![]() ЃЌ
ЃЌ
Ёре§ЗНаЮOABCЕФБпГЄЮЊ5ЃЛ
ЃЈ2ЃЉгаСНжжЧщПіЃК
ЂйQдкOAЩЯЃЌдђCQ=PQЪБФмЙЙГЩСтаЮЃЌ
ЁпPC=2ЃЌ
ЁрAQ=4ЪБВХФмЙЙГЩCQ=PQЕФЕШбќШ§НЧаЮЃЌ
Ёр2k=4ЃЌНтЕУk=2ЃЌ
ЂкQЕудкOCЩЯЃЌЁпЁЯPCQЪЧжБНЧЃЌ
ЁржЛгабиетPQБпЖделВХФмЙЙГЩСтаЮЃЌЧвPC=QCЃЌ
Ёп
ЁрQC=2ЃЌ
Ёр2k=OA+OC-QC=5+5-2=8ЃЌ
Ёрk=4ЃЌ
ЁрЕБk=2Лђk=4ЪБНЋЁїCPQбиЫќЕФвЛБпЗелЃЌЪЙЕУЗелЧАКѓЕФСНИіШ§НЧаЮзщГЩЕФЫФБпаЮЮЊСтаЮЃЛ
ЃЈ3ЃЉЂйЕБЕуAдЫЖЏЕНЕуOЪБЃЌt=3ЃЌ
ЕБ0ЃМtЁм3ЪБЃЌЩшOЁфCЁфНЛxжсгкЕуDЃЌ
дђtanЁЯDOOЁф=![]() ЃЌМД
ЃЌМД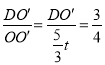 ЃЌ
ЃЌ
ЁрDOЁф=![]() tЃЌ
tЃЌ
ЁрS=![]() DOЁфOOЁф=
DOЁфOOЁф=![]()
![]() t
t![]() t=
t=![]() t2ЃЌ
t2ЃЌ
ЂкЕБЕуCдЫЖЏЕНxжсЩЯЪБЃЌt=ЃЈ5ЁС![]() ЃЉЁТ
ЃЉЁТ![]() =4ЃЌ
=4ЃЌ
ЕБ3ЃМtЁм4ЪБЃЌЩшAЁфBЁфНЛxжсгкЕуEЃЌ
ЁпAЁфO=![]() t-5ЃЌ
t-5ЃЌ
ЁрAЁфE=![]() AЁфO=
AЁфO=![]() ЃЌ
ЃЌ
ЁрS=![]() ЃЈAЁфE+OЁфDЃЉAЁфOЁф=
ЃЈAЁфE+OЁфDЃЉAЁфOЁф=![]() ЃЈAЁфE+OЁфDЃЉAЁфOЁф=
ЃЈAЁфE+OЁфDЃЉAЁфOЁф=![]() ЃЈ
ЃЈ![]() +
+![]() tЃЉ5=
tЃЉ5=![]() ЃЎ
ЃЎ

 ЪюМйЯЮНгНЬВФЦкФЉЪюМйдЄЯАЮфККГіАцЩчЯЕСаД№АИ
ЪюМйЯЮНгНЬВФЦкФЉЪюМйдЄЯАЮфККГіАцЩчЯЕСаД№АИ МйЦкзївЕЪюМйГЩГЄРждАаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИ
МйЦкзївЕЪюМйГЩГЄРждАаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИЁОЬтФПЁПЮТжнФГжабЇ2015бЇФъЦпФъМЖвЛАр40УћЭЌбЇЮЊФГджЧјОшПюЃЌЙВОшПю2000дЊЃЌОшПюЧщПіШчЯТБэЃК
ОшПюЃЈдЊЃЉ | 20 | 40 | 50 | 100 |
ШЫЪ§ | 10 |
| 8 |
БэИёжаОшПю40дЊКЭ50дЊЕФШЫЪ§ВЛаЁаФБЛФЋЫЎЮлШОвбПДВЛЧхГў,ШєЩшОшПю40дЊЕФгаxУћЭЌбЇЃЌОш
Пю50дЊЕФгаyУћЭЌбЇЃЌИљОнЬтвтЃЌПЩЕУЗНГЬзщЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()