题目内容
在△ABC中(1)如图①,∠A=60°,∠B、∠C的平分线交于点P,求∠BPC的度数.
(2)如图②,∠A=60°,∠B、∠C的三等分线交于点P(∠1=
| 1 |
| 3 |
| 1 |
| 3 |
(3)如图③,∠A=x°,∠B、∠C的n等分线(n≥3)交于点P,求∠BPC的度数.
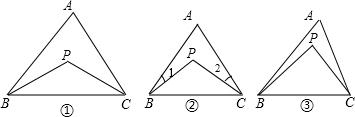
分析:(1)首先根据∠B、∠C的平分线交于点P与△ABC的内角和为180°,求得∠PBC+∠PCB的和,又由△PBC的内角和为180°,求得∠BPC的度数;
(2)首先根据∠B、∠C的三等分线分线交于点P,可得:
∠PBC=∠ABC,
∠PCB=∠ACB,又由△ABC的内角和为180°,求得∠PBC+∠PCB的和,又由△PBC的内角和为180°,求得∠BPC的度数;
(3)首先根据∠B、∠C的三等分线分线交于点P,可得:
∠PBC=∠ABC,
∠PCB=∠ACB,
又由△ABC的内角和为180°,求得∠PBC+∠PCB的和,又由△PBC的内角和为180°,求得∠BPC的度数.
(2)首先根据∠B、∠C的三等分线分线交于点P,可得:
| 3 |
| 2 |
| 3 |
| 2 |
(3)首先根据∠B、∠C的三等分线分线交于点P,可得:
| n |
| n-1 |
| n |
| n-1 |
又由△ABC的内角和为180°,求得∠PBC+∠PCB的和,又由△PBC的内角和为180°,求得∠BPC的度数.
解答:解:(1)∵∠B、∠C的平分线交于点P,
∴2∠PBC=∠ABC,2∠PCB=∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠PBC+2∠PCB=180°,
∵∠A=60°,
∴∠PBC+∠PCB=60°,
∴∠BPC=180°-(∠PBC+∠PCB)=120°;
(2)∵∠1=
∠ABC,∠2=
∠ACB,
∴
∠PBC=∠ABC,
∠PCB=∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴∠A+
∠PBC+
∠PCB=180°,
∵∠A=60°,
∴∠PBC+∠PCB=80°,
∴∠BPC=180°-(∠PBC+∠PCB)=100°;
(3)∵∠B、∠C的n等分线(n≥3)交于点P,
∴
∠PBC=∠ABC,
∠PCB=∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴∠A+
∠PBC+
∠PCB=180°,
∵∠A=x°,
∴∠PBC+∠PCB=
•180°-
•x°,
∴∠BPC=180°-(∠PBC+∠PCB)=180o-
(180o-xo)=
180o+
•xo.
∴2∠PBC=∠ABC,2∠PCB=∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠PBC+2∠PCB=180°,
∵∠A=60°,
∴∠PBC+∠PCB=60°,
∴∠BPC=180°-(∠PBC+∠PCB)=120°;
(2)∵∠1=
| 1 |
| 3 |
| 1 |
| 3 |
∴
| 3 |
| 2 |
| 3 |
| 2 |
∵∠A+∠ABC+∠ACB=180°,
∴∠A+
| 3 |
| 2 |
| 3 |
| 2 |
∵∠A=60°,
∴∠PBC+∠PCB=80°,
∴∠BPC=180°-(∠PBC+∠PCB)=100°;
(3)∵∠B、∠C的n等分线(n≥3)交于点P,
∴
| n |
| n-1 |
| n |
| n-1 |
∵∠A+∠ABC+∠ACB=180°,
∴∠A+
| n |
| n-1 |
| n |
| n-1 |
∵∠A=x°,
∴∠PBC+∠PCB=
| n-1 |
| n |
| n-1 |
| n |
∴∠BPC=180°-(∠PBC+∠PCB)=180o-
| n-1 |
| n |
| 1 |
| n |
| n-1 |
| n |
点评:此题考查了三角形内角和定理与角平分线的性质.解此题的关键是要注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
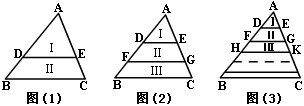

 ,
, 分别是AB、AC的(n+1)等分点,则线段B1C1 + B2C2+……+ BnCn的值是 ______.
分别是AB、AC的(n+1)等分点,则线段B1C1 + B2C2+……+ BnCn的值是 ______. 
 ∠ABC,∠2=
∠ABC,∠2=