题目内容
已知：二次函数y=x2+bx+c与x轴相交于A（x1，0）、B（x2，0）两点，其顶点坐标为P（-
，
），AB=|x1-x2|，若S△APB=1，则b与c的关系式是（ ）A．b2-4c+1=0
B．b2-4c-1=0
C．b2-4c+4=0
D．b2-4c-4=0
【答案】分析：由于抛物线顶点坐标为P（-
，
），AB=|x1-x2|，根据根与系数的关系把AB的长度用b、c表示，而S△APB=1，然后根据三角形的面积公式就可以建立关于b、c的等式．
解答：解：∵x1+x2=-b，x1•x2=c，
∴AB=|x1-x2|=
=
，
∵若S△APB=1
∴S△APB=
=1，
∴-
=1，
∴
=1，
∴
=2，
∴b2-4c-4=0．
故选D．
点评：此题主要考查了抛物线与x轴的交点情况与判别式的关系、抛物线顶点坐标公式、三角形的面积公式等知识，综合性比较强．
，），AB=|x1-x2|，根据根与系数的关系把AB的长度用b、c表示，而S△APB=1，然后根据三角形的面积公式就可以建立关于b、c的等式．解答：解：∵x1+x2=-b，x1•x2=c，
∴AB=|x1-x2|=
=，∵若S△APB=1
∴S△APB=
=1，∴-
=1，∴
=1，∴
=2，∴b2-4c-4=0．
故选D．
点评：此题主要考查了抛物线与x轴的交点情况与判别式的关系、抛物线顶点坐标公式、三角形的面积公式等知识，综合性比较强．
练习册系列答案
相关题目
已知：二次函数的表达式为y=2x2+4x-1．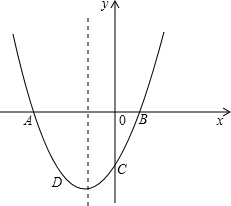
交于点C，点D（-2，-3）在抛物线上．