题目内容
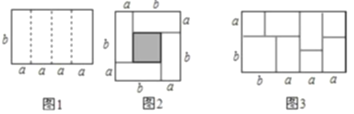
【题目】如图是一个长为![]() 、宽为
、宽为![]() 的长方形,沿中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图).
的长方形,沿中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图).
(1)如图中的阴影部分面积为: ;(用![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)观察如图,请你写出![]() 、
、![]() 、
、![]() 之间的等量关系是 ;
之间的等量关系是 ;
(3)根据(2)中的结论,若![]() ,
,![]() ,则
,则![]() ;
;
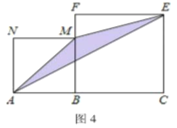
(4)实际上通过计算图形的阴影可以探求相应的等式,如图,请你写出这个等式 ;
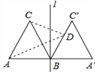
(5)如图,线段![]() (其中
(其中![]() 为正数),点
为正数),点![]() 线在段
线在段![]() 上,在线段
上,在线段![]() 同侧作正方形
同侧作正方形![]() 及正方形
及正方形![]() ,连接
,连接![]() ,
,![]() ,
,![]() 得到
得到![]() .当
.当![]() 时,
时,![]() 的面积记为
的面积记为![]() ;当
;当![]() 时,
时,![]() 的面积记为
的面积记为![]() ;当
;当![]() 时,
时,![]() 的面积记为
的面积记为![]() ;当
;当![]() 时,
时,![]() 的面积记为
的面积记为![]() ,则
,则![]() .
.
【答案】(1) ![]() (2)
(2) ![]() (3) 31;(4)
(3) 31;(4)![]() (5)
(5)![]()
【解析】
(1)阴影部分为边长为(b-a)的正方形,然后根据正方形的面积公式求解;
(2)在图2中,大正方形有小正方形和4个矩形组成,则(a+b)2-(a-b)2=4ab;
(3)由(2)的结论得到(x+y)2-(x-y)2=4xy,再把![]() ,
,![]() 得到
得到![]()
(4)观察图形得到边长为(a+b)与(3a+b)的矩形由3个边长为a的正方形、4个边长为a、b的矩形和一个边长为b的正方形组成,则有(a+b)(3a+b)=3a2+4ab+b2.
(5)根据连接BE,则BE∥AM,利用△AME的面积=△AMB的面积即可得出![]()
![]() 即可得出答案.
即可得出答案.
(1)阴影部分为边长为(ba)的正方形,所以阴影部分的面积![]()
故答案为:![]()
(2)图2中,用边长为a+b的正方形的面积减去边长为ba的正方形等于4个长宽分别a、b的矩形面积,
所以![]()
故答案为:![]()
(3)∵![]()
而![]() ,
,![]()
∴![]()
∴![]()
故答案为:31;
(4)边长为(a+b)与(3a+b)的矩形面积为(a+b)(3a+b),它由3个边长为a的正方形、4个边长为a、b的矩形和一个边长为b的正方形组成,
∴![]()
故答案为:![]()
(5)连接BE.
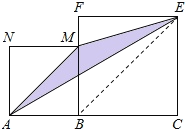
∵在线段AC同侧作正方形ABMN及正方形BCEF,
∴BE∥AM,
∴△AME与△AMB同底等高,
∴△AME的面积=△AMB的面积,
∴当AB=n时,△AME的面积记为![]()
![]()
∴当![]() 时,
时, ![]()
故答案为:![]()