题目内容
对于任意正实数a,b,∵ ≥0,∴a+b﹣2
≥0,∴a+b﹣2 ≥0,∴a+b≥2
≥0,∴a+b≥2 ,只有当a=b时,等号成立.结论:在a+b≥2
,只有当a=b时,等号成立.结论:在a+b≥2 (a,b均为正实数)中,若ab为定值p,则a+b≥2
(a,b均为正实数)中,若ab为定值p,则a+b≥2 只有当a=b时,a+b有最小值2
只有当a=b时,a+b有最小值2 .根据上述内容,回答下列问题:若m>0,只有当m=_________,m+
.根据上述内容,回答下列问题:若m>0,只有当m=_________,m+ 有最小值_______。
有最小值_______。
 ≥0,∴a+b﹣2
≥0,∴a+b﹣2 ≥0,∴a+b≥2
≥0,∴a+b≥2 ,只有当a=b时,等号成立.结论:在a+b≥2
,只有当a=b时,等号成立.结论:在a+b≥2 (a,b均为正实数)中,若ab为定值p,则a+b≥2
(a,b均为正实数)中,若ab为定值p,则a+b≥2 只有当a=b时,a+b有最小值2
只有当a=b时,a+b有最小值2 .根据上述内容,回答下列问题:若m>0,只有当m=_________,m+
.根据上述内容,回答下列问题:若m>0,只有当m=_________,m+ 有最小值_______。
有最小值_______。1,2

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
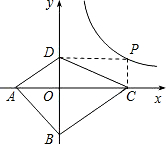
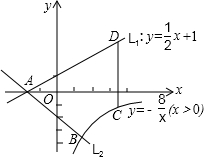 时,点A、B、C、D围成的四边形面积.
时,点A、B、C、D围成的四边形面积.