��Ŀ����
��֪���κ���y=x2+px+qͼ��Ķ���MΪֱ��y=
x��y=-x+m�Ľ��㣬
��1���ú�m�Ĵ���ʽ����ʾ��M�����ꣻ
��2�������κ���y=x2+px+qͼ��A��0��3��������κ���y=x2+px+q�Ľ���ʽ��
��3���ڣ�2���еĶ��κ���y=x2+px+q��ͼ����x�����������㣬����x�����ΪB����PΪ�����߶Գ�����һ�㣬����PABΪֱ�������Σ�������������������ĵ�P�����꣮
| 1 | 2 |
��1���ú�m�Ĵ���ʽ����ʾ��M�����ꣻ
��2�������κ���y=x2+px+qͼ��A��0��3��������κ���y=x2+px+q�Ľ���ʽ��
��3���ڣ�2���еĶ��κ���y=x2+px+q��ͼ����x�����������㣬����x�����ΪB����PΪ�����߶Գ�����һ�㣬����PABΪֱ�������Σ�������������������ĵ�P�����꣮
��������1����ֱ֪��y=
x��y=-x+m���г��������x��y�ĵ�����ϵʽ���������M�����꣮
��2����A���������y=(x-
m)2+
m�����m��ֵ���ɵó�����ʽ��
��3�����âٵ���BAP=90��ʱ���ڵ���ABP=90��ʱ���۵���APB=90��ʱ���ֱ���P�����꼴�ɣ�
| 1 |
| 2 |
��2����A���������y=(x-
| 2 |
| 3 |
| 1 |
| 3 |
��3�����âٵ���BAP=90��ʱ���ڵ���ABP=90��ʱ���۵���APB=90��ʱ���ֱ���P�����꼴�ɣ�
����⣺��1����
��
��
��
������M������
m��
m����
��2���ߴ�ʱ���κ���Ϊy=(x-
m)2+
m����A��0��3����
��3=(0-
m)2+
m��
��m1=-3��m2=
��
��y=��x+2��2-1����y=(x-
)2+
��
��3���߶��κ���y=(x-
)2+
��x��û�н��㣬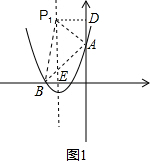
�֡߶��κ���y=x2+px+q��ͼ����x������������ʱ��
����κ���Ϊy=x2+4x+3����x�����BΪ��-3��0�����Գ���Ϊֱ��x=-2
�ٵ���BAP=90��ʱ����ͼ1����P1D��y���ڵ�D��
��P������Ϊ��-2��y������P1A2+AB2=BP12���ɵ�P1D2+AD 2+AB2=P1E2+BE 2��
��22+��y-3��2+��3
��2=y2+12��
��ã�y=5��
�ɵ�P1����Ϊ��-2��5����
�ڵ���ABP=90��ʱ����ͼ2����BP2 2+AB2=AP2 2����P������Ϊ��-2��a����
��a2+1+��3
��2=��3-a��2+��-2��2
��ã�a=-1��
�ɵ�P2����Ϊ��-2��-1����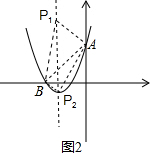
�۵���APB=90��ʱ��ͬ���ɵ�P1A2+BP12=AB2����P������Ϊ��-2��b����
��3
��2=��b-3��2+4+1+b2��
��ã�b=
��
��
�ɵ�P����ABΪֱ����Բ��ֱ��x=-2�Ľ����ϣ���������
P3��-2��
+
����P4��-2��
-
����
���ϵã���PΪ��-2��5������-2��-1������-2��
+
����-2��
-
��ʱ����PABΪֱ�������Σ�
|
��
|
������M������
| 2 |
| 3 |
| 1 |
| 3 |
��2���ߴ�ʱ���κ���Ϊy=(x-
| 2 |
| 3 |
| 1 |
| 3 |
��3=(0-
| 2 |
| 3 |
| 1 |
| 3 |
��m1=-3��m2=
| 9 |
| 4 |
��y=��x+2��2-1����y=(x-
| 3 |
| 2 |
| 3 |
| 4 |
��3���߶��κ���y=(x-
| 3 |
| 2 |
| 3 |
| 4 |

�֡߶��κ���y=x2+px+q��ͼ����x������������ʱ��
����κ���Ϊy=x2+4x+3����x�����BΪ��-3��0�����Գ���Ϊֱ��x=-2
�ٵ���BAP=90��ʱ����ͼ1����P1D��y���ڵ�D��
��P������Ϊ��-2��y������P1A2+AB2=BP12���ɵ�P1D2+AD 2+AB2=P1E2+BE 2��
��22+��y-3��2+��3
| 2 |
��ã�y=5��
�ɵ�P1����Ϊ��-2��5����
�ڵ���ABP=90��ʱ����ͼ2����BP2 2+AB2=AP2 2����P������Ϊ��-2��a����
��a2+1+��3
| 2 |
��ã�a=-1��
�ɵ�P2����Ϊ��-2��-1����

�۵���APB=90��ʱ��ͬ���ɵ�P1A2+BP12=AB2����P������Ϊ��-2��b����
��3
| 2 |
��ã�b=
| 3 |
| 2 |
| ||
| 2 |
�ɵ�P����ABΪֱ����Բ��ֱ��x=-2�Ľ����ϣ���������
P3��-2��
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
���ϵã���PΪ��-2��5������-2��-1������-2��
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
���������⿼����Ƕ��κ������ۺ������Լ�ֱ�������ε����ʵ�֪ʶ�����÷������۵ó�P�������ǽ���ؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
��֪���κ���y=x2+��2a+1��x+a2-1����СֵΪ0����a��ֵ�ǣ�������
A��
| ||
B��-
| ||
C��
| ||
D��-
|
 ��֪���κ���y=-x2+2x+m�IJ���ͼ����ͼ��ʾ�������x��һԪ���η���-x2+2x+m=0�Ľ�Ϊ��������
��֪���κ���y=-x2+2x+m�IJ���ͼ����ͼ��ʾ�������x��һԪ���η���-x2+2x+m=0�Ľ�Ϊ��������| A��x1=1��x2=3 | B��x1=0��x2=3 | C��x1=-1��x2=1 | D��x1=-1��x2=3 |
 ��֪���κ���y=-x2+bx+c��ͼ����ͼ��ʾ������x���һ����������Ϊ��-1��0������y��Ľ�������Ϊ��0��3����
��֪���κ���y=-x2+bx+c��ͼ����ͼ��ʾ������x���һ����������Ϊ��-1��0������y��Ľ�������Ϊ��0��3����