题目内容
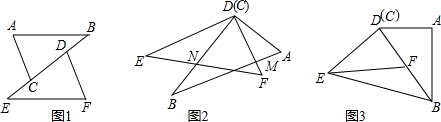
如所示，已知在△ABC和△CEF中，∠BCE=∠ACF，EC=BC．试说明：AB=EF．
解：∵∠BCE=∠ACF，
∴∠BCE+∠BCF=∠ACF+∠BCF，
即∠ACB=∠ECF，
在△ABC和△CEF中，
，
∴△ABC≌△CEF（ASA），
∴AB=EF．
分析：先求出∠ACB=∠ECF，再结合已知条件证明△ABC和△CEF全等，然后根据全等三角形对应边相等即可证明AB=EF．
点评：本题主要考查全等三角形的判定，证明∠ACB=∠ECF是解题的关键．
∴∠BCE+∠BCF=∠ACF+∠BCF，
即∠ACB=∠ECF，
在△ABC和△CEF中，
，∴△ABC≌△CEF（ASA），
∴AB=EF．
分析：先求出∠ACB=∠ECF，再结合已知条件证明△ABC和△CEF全等，然后根据全等三角形对应边相等即可证明AB=EF．
点评：本题主要考查全等三角形的判定，证明∠ACB=∠ECF是解题的关键．
练习册系列答案
相关题目
如所示，已知在△ABC和△CEF中，∠BCE=∠ACF，EC=BC．试说明：AB=EF．
19、如图所示，已知在△ABC中，∠B=90°，点D、点E分别在BC和AB上．求证：AD2+CE2=AC2+DE2．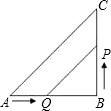
点P从点B开始沿BC边向点C以2cm/s的速度移动．