题目内容
（2013•嘉定区一模）已知：点D是Rt△ABC的BC边的一个动点（如图），过点D作DE⊥AB，垂足为E，点F在AB边上（点F与点B不重合），且满足FE=BE，联结CF、DF．
（1）当DF平分∠CFB时，求证：
=
：
（2）若AB=10，tanB=
．当DF⊥CF时，求BD的长．
（1）当DF平分∠CFB时，求证：
| CF |
| CB |
| BD |
| FB |
（2）若AB=10，tanB=
| 3 |
| 4 |
分析：（1）利用由两对角相等的三角形相似即可证明△CFD∽△CBF，由相似三角形的性质：对应边的比值相等即可证明
=
；
（2）利用已知条件可求出AC=6，BC=8，因为tanB=
．可设DE=3x，则BE=4x，则BD=5x，CD=BC-BD=8-5x，再证明三角形ACF是等腰三角形，进而得到CF=6，根据勾股定理建立方程求出x的值即可．
| CF |
| CB |
| BD |
| FB |
（2）利用已知条件可求出AC=6，BC=8，因为tanB=
| 3 |
| 4 |
解答：（1）证明：∵DF平分∠CFB，
∴∠CFD=∠EFD，
∵DE⊥AB，FE=BE，
∴DF=BD，
∴∠EFD=∠DBF，
∵∠FCD=∠BCF，
∴△CFD∽△CBF，
∴
=
，
∵DF=BD，
∴
=
；
（2）解：∵AB=10，tanB=
，
∴AC=6，BC=8，
∵tanB=
．设DE=3x，则BE=4x，则BD=5x，CD=BC-BD=8-5x，
∵DE⊥AB，FE=BE，
∴DF=BD，
∴∠DFB=∠B，
∵DF⊥CF，
∴∠AFC+∠BFD=90°，
∵∠A+∠B=90°，
∴∠A=∠AFC，
∴AC=FC=6，
∴62+（5x）2=（8-5x）2，
解得：x=
，
故当DF⊥CF时，BD的长是
．
∴∠CFD=∠EFD，
∵DE⊥AB，FE=BE，
∴DF=BD，
∴∠EFD=∠DBF，
∵∠FCD=∠BCF，
∴△CFD∽△CBF，
∴
| CF |
| CB |
| FD |
| FB |
∵DF=BD，
∴
| CF |
| CB |
| BD |
| FB |
（2）解：∵AB=10，tanB=
| 3 |
| 4 |
∴AC=6，BC=8，
∵tanB=
| 3 |
| 4 |
∵DE⊥AB，FE=BE，
∴DF=BD，
∴∠DFB=∠B，
∵DF⊥CF，
∴∠AFC+∠BFD=90°，
∵∠A+∠B=90°，
∴∠A=∠AFC，
∴AC=FC=6，
∴62+（5x）2=（8-5x）2，
解得：x=
| 7 |
| 20 |
故当DF⊥CF时，BD的长是
| 7 |
| 4 |
点评：本题考查了直角三角形的性质、相似三角形的判定和性质、勾股定理的运用、等腰三角形的判定和性质以及锐角三角函数的应用，题目的综合性很好，难度中等．
练习册系列答案
相关题目
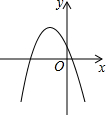（2013•嘉定区一模）已知抛物线y=-x2+bx+c如图所示，那么b、c的取值范围是（ ）